数学
设随机变量X服从（-1，1）上的均匀分布，事件A={0A、P（AB）=0B、P（AB）=P（A）C、P（A）+P（B）=1D、P（AB）=P（A）P（B）
题目
设随机变量X服从（-1，1）上的均匀分布，事件A={0
- A、P（AB）=0
- B、P（AB）=P（A）
- C、P（A）+P（B）=1
- D、P（AB）=P（A）P（B）
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设两个相互独立的随机变量X和Y分别服从正态分布N(0，1)和N(1，1)，则
答案：B
解析：
【简解】首先应看到，X+Y和X-Y均为一维正态分布的随机变量.其次要看到，如果z～N(μ，σ^2)，则
，反之，如果
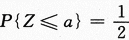，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.
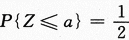，反之，如果，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.
第2题：
设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.
答案：
解析：
第3题：
设平面区域D由曲线y=1／x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
参考答案：
第4题：
设随机变量(X,Y)在区域D={(z,y)｜0≤x≤2,0≤y≤1}上服从均匀分布,令
U=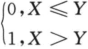
,V=
.
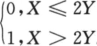(1)求(U,V)的联合分布；(2)求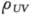
.
U=
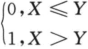,V=.
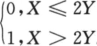(1)求(U,V)的联合分布；(2)求
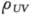.答案：
解析：
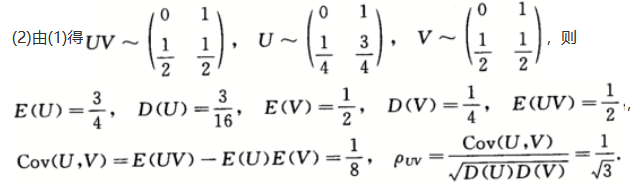
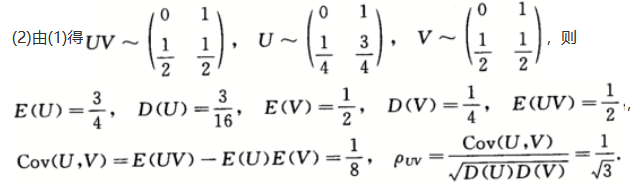
第5题：
设X1,X2,…,X100相互独立且在区间［－1,1］上同服从均匀分布,则由中心极限定理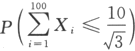
≈_______.
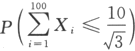≈_______.答案：1、0.841 3
解析：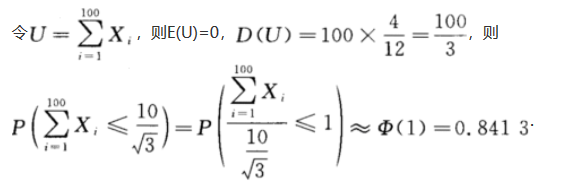
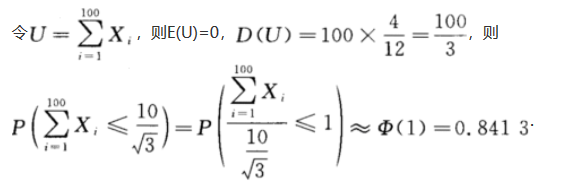
第6题：
设随机变量X,Y相互独立,且X～N(0,1),Y～N(1,1),则().
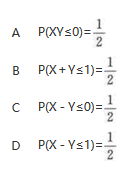
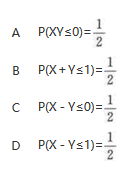
答案：B
解析：
X，Y独立，X～N(0，1)，Y～N(1，1)，X+Y～N(1，2)
P(X+Y≤1)=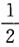
，所以选(B).
P(X+Y≤1)=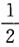，所以选(B).第7题：
设随机变量X在［-1,2］上服从均匀分布,随机变量=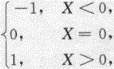
则D(Y)=_______.
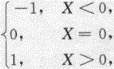则D(Y)=_______.答案：
解析：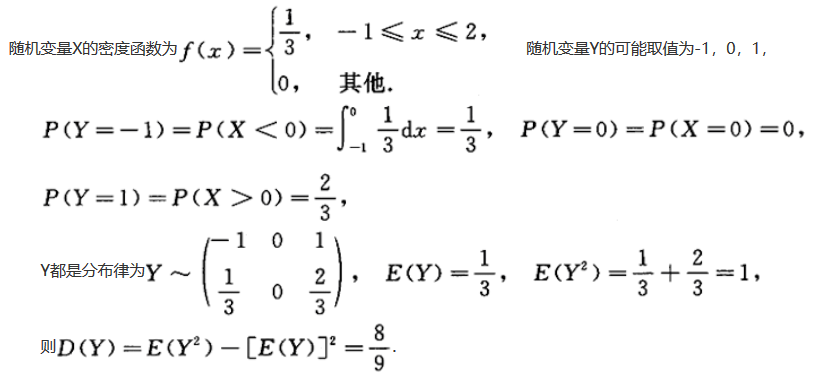
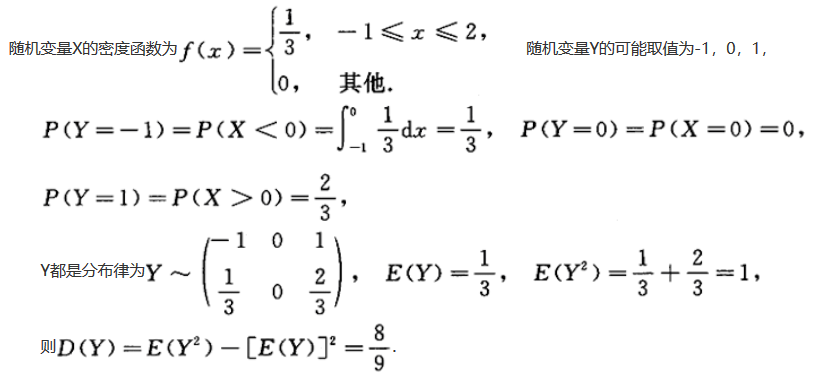
第8题：
设随机变量X服从[-3，3]上的均匀分布，则
P(0＜X≤4)为( )。
A．2/3
B．1/2
C．3/4
D．1
正确答案：B
解析：(1)P0X≤4)＝(3-0)/6＝1/2；
解析：(1)P0X≤4)＝(3-0)/6＝1/2；
第9题：
设随机变量X服从参数为2的指数分布,证明：Y=1-
在区间(0,1)上服从均匀分布.
在区间(0,1)上服从均匀分布.答案：
解析：
第10题：
设随机变量X在区间(0，1)内服从均匀分布，在X=x(0
(Ⅱ)Y的概率密度；
(Ⅲ)概率P{X+Y>1}.
(Ⅱ)Y的概率密度；
(Ⅲ)概率P{X+Y>1}.
答案：
解析：
【简解】本题是数四2004年考题，考查均匀分布，二维随机变量的概率密度、边缘密度和条件密度，当年的得分率仅为0.204.主要的困难在于对条件概率密度的理解.
