数学
考虑对正态总体的均值进行双侧假设检验，如果在显著性水平α1=0.05下接受原假设H0：μ=μ0，则在显著性水平α2=0.01下（）A、必然拒绝H0B、必然接受H0C、接受H0的概率为0.01D、拒绝H0的概率为0.05
题目
考虑对正态总体的均值进行双侧假设检验，如果在显著性水平α1=0.05下接受原假设H0：μ=μ0，则在显著性水平α2=0.01下（）
- A、必然拒绝H0
- B、必然接受H0
- C、接受H0的概率为0.01
- D、拒绝H0的概率为0.05
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
单侧检验指按分布的一侧计算显著性水平概率的检验,用于检验大于,小于有确定性大小关系的假设检验问题,假设检验写作:μ1μ2。双侧检验指按分布两端计算显著性水平概率的检验。用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验写作h1:μ1≠μ2。()
此题为判断题(对，错)。
参考答案：正确
第2题：
在假设检验中，方差已知的正态总体均值的检验要计算Z统计量。()
答案：(错)
第3题：
当对正态总体均值检验时，如果总体方差未知则应该进行（ ）。
A．Z检验
B．F检验
C．t检验
D．卡方检验
正确答案：C
第4题：
对某一总体均值进行假设检验，H0：μ=100，H1：μ≠100。检验结论是：在1%的显著性水平下，应拒绝H0。据此可认为对原假设进行检验的P值小于1%。（ ）
答案：对
解析：
P值检验的原理是：建立原假设后，在假定原假设成立的情况下，参照备选假设，可以计算出检验统计量超过或者小于由样本所计算出的检验统计量的数值的概率，这便是P值。而后将此P值与事先给出的显著性水平a进行比较，如果P值小于a，也就是说，原假设对应的为小概率事件，根据小概率原理，就可以否定原假设，而接受对应的备选假设；如果P值大于a，就不能否定原假设。题中检验结论是在1%的显著性水平下拒绝H0，所以P值小于显著性水平1%。
第5题：
下面关于单侧和双侧假设检验的说法，正确的有（ ）。
A.在显著性水平a下，检验假设H0：μ=μ0；H1：μ≠μ0。的假设检验，称为双侧假设检验
B.右侧检验和左侧检验统称为单侧检验
C.在显著性水平a下，检验假设H0：μ≥μ0；H1：μ<μ0的假设检验，称为左侧检验
D.在显著性水平a下，检验假设H0：μ≥μ0；H1：μ<μ0的假设检验，称为右侧检验
E.在显著性水平a下，检验假设H0：H0≤μ0；H1：μ>μ0的假设检验，称为右侧检验
B.右侧检验和左侧检验统称为单侧检验
C.在显著性水平a下，检验假设H0：μ≥μ0；H1：μ<μ0的假设检验，称为左侧检验
D.在显著性水平a下，检验假设H0：μ≥μ0；H1：μ<μ0的假设检验，称为右侧检验
E.在显著性水平a下，检验假设H0：H0≤μ0；H1：μ>μ0的假设检验，称为右侧检验
答案：A,B,C,E
解析：
假设检验分为：①双侧检验H0:μ=μ0；H1：μ≠μ0；②单侧检验。右侧检验H0：μ≤μ0；H1：μ>μ0；左测检验H0：μ≥μ0；H1：μ<／μ0。
第6题：
在假设检验中，下面的说法正确的是( )。
A．建立假设时，有原假设H0和备择假设H1
B．已知μ0，可假设H0:μ=μ0，H1:μ≠μ0检验样本均值是否为μ0
C．正态总体σ己知时，μ的显著性水平为α的检验采用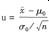
作为检验统计量
D．假设H0:μ≤μ0，H1:μ＞μ0，是双侧假设检验
E．假设H0:μ=μ0，H1:μ≠μ0，是双侧假设检验
正确答案：ABCE
解析：对假设H0:μ≤μ0，备择假设H1:μ＞μ0，是单侧假设检验。
解析：对假设H0:μ≤μ0，备择假设H1:μ＞μ0，是单侧假设检验。
第7题：
在对总体均值进行假设检验时，采用什么检验统计量取决于所抽取的样本是大样本还是小样本，还需要考虑总体是否为正态分布、总体方差是否已知等。（ ）
答案：对
解析：
第8题：
当对正态总体均值检验时，如果总体方差未知则应该进行( )。
A．Z检验
B．F检验
C．t检验
D．χ2检验
正确答案：C
解析：A项适用于总体方差σ2已知，关于总体均值μ的检验；B项适用于两个正态总体方差之比的检验；D项适用于一个正态总体方差σ2的检验。
解析：A项适用于总体方差σ2已知，关于总体均值μ的检验；B项适用于两个正态总体方差之比的检验；D项适用于一个正态总体方差σ2的检验。
第9题：
当对正态总体均值检验时，如果总体方差未知，在小样本情况下应采用（）。
A.z检验
B.F检验
C.t检验
D.X2检验
B.F检验
C.t检验
D.X2检验
答案：C
解析：
当对正态总体均值检验时，如果总体方差未知，在小样本情况下，应采用t检验；在大样本情况下，采用2检验。
第10题：
下面关于单侧和双侧假设检验的说法，正确的有（）。
A.在显著性水平a下，检验假设H0：μ=μ0；H1：μ≠μ0的假设检验，称为双侧假设检验
B.右侧检验和左侧检验统称为单侧检验
C.在显著性水平a下，检验假设H0：μ≥μ0；H1：μ<μ0的假设检验，称为左侧检验
D.在显著性水平a下，检验假设H0：μ>／μ0；H1：μ<μ0的假设检验，称为右侧检验
E.在显著性水平a下，检验假设H0：μ=μ0；H1：μ>μ0的假设检验，称为右侧检验
B.右侧检验和左侧检验统称为单侧检验
C.在显著性水平a下，检验假设H0：μ≥μ0；H1：μ<μ0的假设检验，称为左侧检验
D.在显著性水平a下，检验假设H0：μ>／μ0；H1：μ<μ0的假设检验，称为右侧检验
E.在显著性水平a下，检验假设H0：μ=μ0；H1：μ>μ0的假设检验，称为右侧检验
答案：A,B,C,E
解析：
假设检验分为：①双侧检验H0：μ=μ0；H1：μ≠μ0；②单侧检验。右侧检验H0：μ≤μ0；H1：μ>μ0；左侧检验H0：μ≥μ0；H1：μ<μ0。