数字5用浮点表示,则指数部分位表示为()A、2^(K-1)+1B、2^K+1C、2^(K-1)D、2^K
题目
数字5用浮点表示,则指数部分位表示为()
- A、2^(K-1)+1
- B、2^K+1
- C、2^(K-1)
- D、2^K
相似问题和答案
第1题:
某计算机字长为32位,浮点表示时,阶码占8位,尾数占24位(各包含 l位符号位),阶码用补码表示,尾数用原码表示,该浮点数能表示的最大正数是(5),能表示的最小负数是(6)。
A.(1-2-23)×27
B.(1-2-23)×(27-1)
C.(1-2-24)×27-1
D.-(1-2-23)×27
第2题:
列关于计算机中数的表示的叙述中,错误的是
A.正整数无论采用原码、反码或补码表示,其编码都相同
B.实数的浮点表示法由指数和尾数(含符号位)两部分组成
C.实数都能用浮点形式精确表示
D.整数也能用浮点数形式表示
解析:实数可以用浮点数表示。浮点的表示范围虽然很大,但运算中还是可能出现超出它允许范围的一些结果,这种情况称为“向上溢出”。浮点数能表示绝对值很小的数,当运算中出现绝对值更小的数时,这种情况称为“向下溢出””,这时,处理器只能用0来表示。
第3题:
设浮点数字长16位,其中阶码5位(含1位阶符),以2为底补码表示,尾数11位(含1位数符)补码表示,下列十进制数表示成规格化浮点数为多少?
设浮点数字长16位,其中阶码5位(含1位阶符),以2为底补码表示,尾数11位(含1位数符)补码表示,下列十位进制数表示成规化浮点数为多少?
3.5:(1);79/512:(2);-10-4:(3);1010:(4)
A.不能表示成浮点数
B.11110 01001111000
C.10010 01110000000
D.11101 10111111110
第4题:
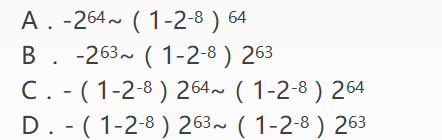
B.B
C.C
D.D

第5题:


第6题:
用12位寄存器表示规格化浮点数,左4位为阶码(含1位符号),右8位为尾数(含1尾符),阶码用移码,尾数用补码表示时,(-40)10表示成规定的浮点数是(2)。
A.
B.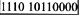
C.
D.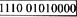
解析:浮点数中尾数最高位的真值为1的浮点数称为规格化浮点数。将浮点数规格化的方法是调整阶码使尾数满足下列关系:尾数为原码表示时,无论正负应满足1/2<|d|1,即小数点后的第一位数一定要为1。正数的尾数应为0.1x…x,负数的尾数应为1.1x…x。尾数用补码表示时,小数最高位应与数符符号位相反。正数应满足1/2d1,即0.1x…x;负数应满足-1/2>d-1,即1.0x…x。(-40)10=-(0.101000)2×2+6,阶码6用移码表示为1110,尾数-0.101000用补码表示为1011000,尾数为8位所以加补一位0,因此选B。
第7题:


第8题:
用8位寄存器表示浮点数,左3位为阶码(含1位符号),右5位为尾数(含1尾符),阶码用移码,尾数用补码表示时,(-3.25)10的浮点数形式是(1)。
A.
B.
C.
D.
解析:(-3.25)10=-0.1101×2+2,阶码2用移码表示为110,尾数-0.1101用补码表示为10011,所以选A。
第9题:
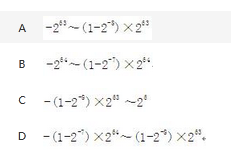

第10题:
浮点数的表示精度由浮点数的哪部分决定()。
- A、尾数
- B、指数
- C、尾数和指数
- D、基数
正确答案:A
