水利水电工程
设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）。A、mR2B、mR2/2C、mRω
题目
设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）。
- A、mR2
- B、mR2/2
- C、mRω
参考答案和解析
正确答案:B
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
偏心轮为均质圆盘，其质量为m，半径为R，偏心距OC=R/2。若在图示位置时，轮绕O轴转动的角速度为ω，角加速度为α，则该轮的惯性力系向O点简化的主矢FI和主矩MIO的大小为：
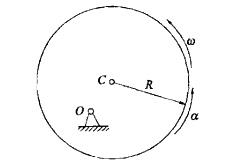
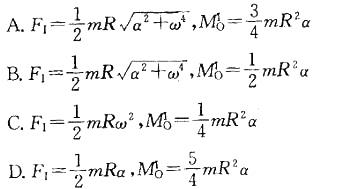
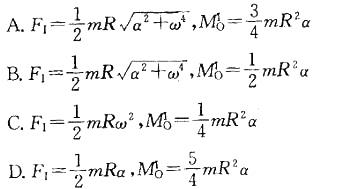
答案：A
解析：
提示：MIO=-JOα，其中 JO = JC + m* OC2 。
第2题：
均质圆盘质量为m，半径为R，在铅垂平面内绕O轴转动，图示瞬时角速度为ω，则其对O轴的动量矩和动能大小分别为：
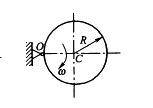
答案：D
解析：
第3题：
有一半径为R的匀质水平圆转台,绕通过其中心且垂直圆台的轴转动,转动惯量为J,开始时有一质量为m的人站在转台中心,转台以匀角速度w0转动,随后人沿着半径向外跑去,当人到达转台边缘时,转台的角速度为()
A、w0
B、Jw0/mR^2
C、Jw0/(J+mR^2)
D、Jw0/(J+2mR^2)
参考答案：C
第4题：
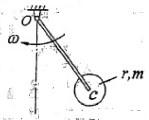
忽略质量的细杆OC=l，其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m，半径为r。系统以角速度ω绕轴O转动，如图所示。系统的动能是：
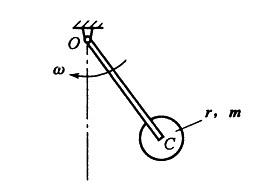
答案：D
解析：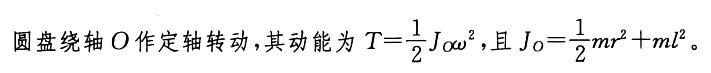
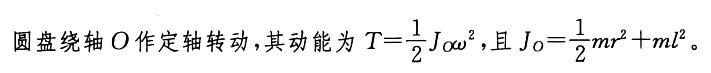
第5题：
图示质量为m、长为l的杆OA以的角速度绕轴O转动，则其动量为：
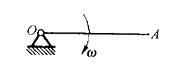
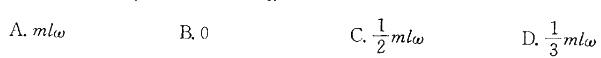
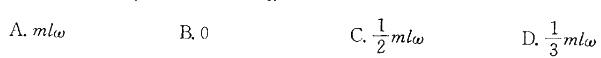
答案：C
解析：
提示：根据动量的公式：p=mvc。
第6题：
均质圆柱体半径为R，质量为m，绕关于对纸面垂直的固定水平轴自由转动，初瞬时静止（G在O轴的铅垂线上），如图所示。则圆柱体在位置θ=90°时的角速度是（ ）。
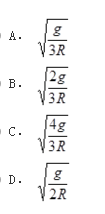
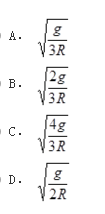
答案：C
解析：
第7题：
图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆盘中心O的水平轴转动，角速度为ω，角加速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为（ ）。
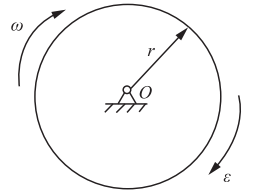
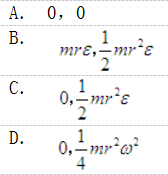
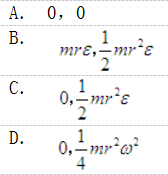
答案：C
解析：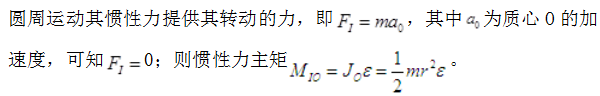
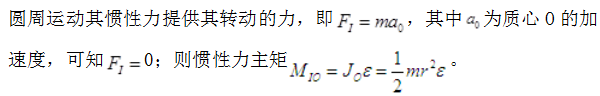
第8题：
等角速度ω旋转容器,半径为R,内盛有密度为ρ的液体,则旋转前后容器底压强分布();
A.相同;
B.不相同;
参考答案：B
第9题：
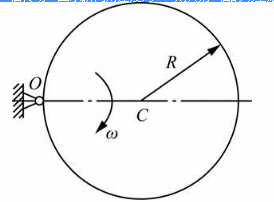
均质圆盘质量为m，半径为R，在铅垂面绕内O轴转动，图示瞬间角速度为ω，则其对O轴的动量矩大小为（ ）。
A．mRω
B．mRω/2
C．mR2ω/2
D．3mR2ω/2
B．mRω/2
C．mR2ω/2
D．3mR2ω/2
答案：D
解析：
根据质点的动量矩公式，体系对O点的动量矩为：
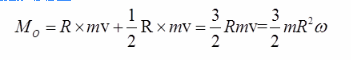
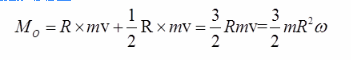
第10题：
忽略质量的细杆OC=l,其端部固结匀质圆盘圆心，盘质量为m,半径为r。系统以角速度w绕轴O转动。系统的动能是：
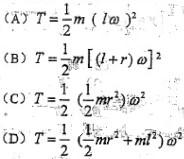
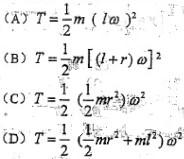
答案：D
解析：
此为定轴转动刚体，动能表达式为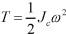
，其中Jc为刚体通过质心且垂直于运动平面
的轴的转动惯量。
此题中，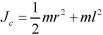
，带入动能表达式，选（D）。
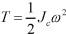，其中Jc为刚体通过质心且垂直于运动平面
的轴的转动惯量。
此题中，
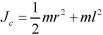，带入动能表达式，选（D）。