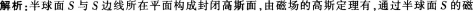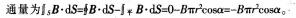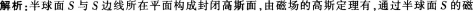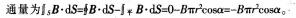设匀强电场的场强E与半径为R的半球面的对称轴平行,计算通过此半球面的电场强度通量。
题目
设匀强电场的场强E与半径为R的半球面的对称轴平行,计算通过此半球面的电场强度通量。
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
如图,半径为a,电荷线密度ρL(r)为常数的均匀带电圆环在轴线上的电场强度为( )。
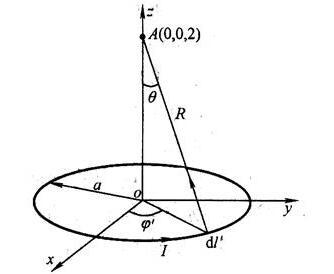
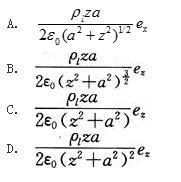

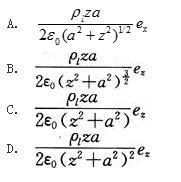
答案:A
解析:
根据点对点的场强公式,圆环上一点对轴线的场强为:


第2题:
在真空中,有一半径为R的均匀带电球面,面密度为σ,球心处的电场强度为( )。
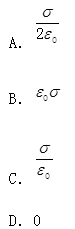
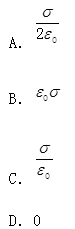
答案:D
解析:
带电球面为等位体,并且电荷在球面上均匀分布,根据对称性可知,球心处场强为0。
第3题:
下面说法正确的是():
A、若穿过一闭合曲面的电场强度通量不为零,则此闭合曲面上电场强度处处不为零
B、若穿过一闭合曲面的电场强度通量为零,则此闭合曲面上电场强度处处为零
C、若一高斯面内没有净电荷,则此高斯面上每一点的电场强度E必为零
D、若一高斯面内没有净电荷,则穿过此高斯面的电场强度通量必为零
参考答案:D
第4题:
半径为R的均匀带电球面,若其电荷面密度为σ,则在距离球面R处的电场强度大小为( )。
A.
B.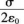
C.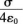
D.
A.

B.
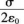
C.
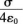
D.

答案:C
解析:

第5题:
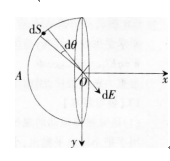
一半径为R的半球面,均匀地分布着电荷面密度为盯的电荷,则球心处的电场强度是多少
答案:
解析:
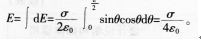

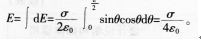

第6题:
在真空中,半径为R的均匀带电半球面,其面电荷密度为σ,该半球面球心处的电场强度值为( )。
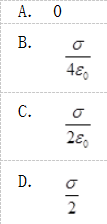
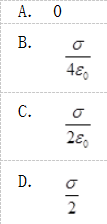
答案:B
解析:

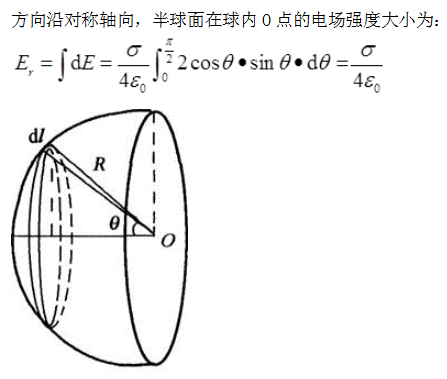



第7题:
真空中有一均匀带电球表面,半径为R,电荷总量为q,则球心处的电场强度大小应为下列哪项数值?( )
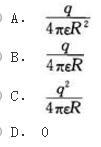
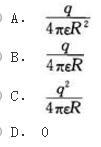
答案:D
解析:
带电球体中心场强为0,分析如下取中性点半径为r的小球,其场强为:
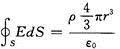
解得
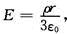
当 r→0时的极限,即电场强度E=0。
【说明】根据高斯定理,在任意闭合曲面上,电位移向量的面积积分恒等于该闭合曲面内所有自由电荷的代数和,已知带电球面的自由电荷只是分布在表面,内部没有自由电荷,因此球心处的电场强度为0。这种现象又称为静电屏蔽效应,带电球面的中心处电场强度为0。
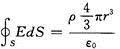
解得
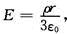
当 r→0时的极限,即电场强度E=0。
【说明】根据高斯定理,在任意闭合曲面上,电位移向量的面积积分恒等于该闭合曲面内所有自由电荷的代数和,已知带电球面的自由电荷只是分布在表面,内部没有自由电荷,因此球心处的电场强度为0。这种现象又称为静电屏蔽效应,带电球面的中心处电场强度为0。
第8题:
在匀强电场中场强等于沿场强方向每单位长度上的电势差。()
此题为判断题(对,错)。
参考答案:正确
第9题:
在Oyz平面内有一半径为R的圆环,均匀带有电荷量q,试计算圆环轴线(ox轴)上任意一点P处的电场强度及电势的大小。
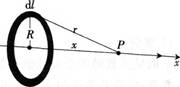

答案:
解析:



第10题:
在磁感强度为B的均匀磁场中作一半径为r的半球面s,s边线所在平面的法线方向单位矢量n与B的夹角为仅,则通过半球面s的磁通量(取弯面向外为正)为()。


A.r2B
B.2r2B
C.-πr2Bsinα
D.-πr2Bcosα
B.2r2B
C.-πr2Bsinα
D.-πr2Bcosα
答案:D
解析: