单选题已知某一活动i→j开始的最早时间ESi,j=3,该活动的作业时间为5,则结点j的最迟时间LFj为()。A 3B 8C 不确定D 2
题目
3
8
不确定
2
相似问题和答案
第1题:
活动i-j对最早可能开始时间等于事件i的最迟必须发生时间。()
第2题:
事件j的最早时间TE(j)是指
A、以事件j为开工事件的工序最早可能开工时间
B、以事件j为完工事件的工序最早可能结束时间
C、以事件j为开工事件的工序最迟必须开工时间
D、以事件j为完工事件的工序最迟必须结束时间
第3题:
已知某工作i-j的持续时间为6d,其中i节点的最早开始时间为第18d,最迟开始时间为第23d,则该工作的最早完成时间为( )d。
A.18
B.21
C.24
D.25
第4题:
B.21天
C.23天
D.26天
最早完成时间等于最早开始时间加上其持续时间:18+5-23.。
第5题:
A.工作i的最迟完成时间与工作i的最早完成时间之差
B.工作i的最迟开始时间与工作i的最早开始时间之差
C.工作i的最早完成时间与工作j的最迟开始时间之差
D.工作i与工作j的时间间隔加上j工作的总时差
E.工作i的最早完成时间与工作j的最迟开始时间之和
第6题:
活动i-j的最迟必须开始时间等于事件i的最迟必须发生时间。()
第7题:
如图5-5所示的活动图中,从A到J的关键路径是(1),I和J之间的活动开始的最早时间是(2)。
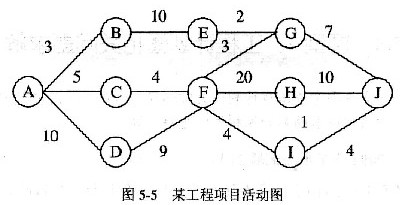
(1)
A.ABEGJ
B.ADFHJ
C.ACFGJ
D.ADFIJ
第8题:
在下面的活动图中,从A到J的关键路径是(24),I和J之间的活动开始的最早时间是(25)。
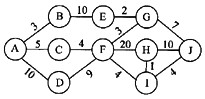
A.ABEGJ
B.ADFHJ
C.ACFGJ
D.ADFIJ
解析:见公共试题Ⅲ(23)、(24)。
第9题:
B 宽度优先(种子染色法)
5.关键路径
几个定义: 顶点1为源点,n为汇点。
a. 顶点事件最早发生时间Ve[j], Ve [j] = max{ Ve [j] + w[I,j] },其中Ve (1) = 0;
b. 顶点事件最晚发生时间 Vl[j], Vl [j] = min{ Vl[j] – w[I,j] },其中 Vl(n) = Ve(n);
c. 边活动最早开始时间 Ee[I], 若边I由<j,k>表示,则Ee[I] = Ve[j];
d. 边活动最晚开始时间 El[I], 若边I由<j,k>表示,则El[I] = Vl[k] – w[j,k];
若 Ee[j] = El[j] ,则活动j为关键活动,由关键活动组成的路径为关键路径。
求解方法:
a. 从源点起topsort,判断是否有回路并计算Ve;
第10题:
B.工作J的最早开始时间与工作i的最早完成时间之差
C.工作i与工作j的时间间隔加上工作j的总时差
D.工作i的最迟开始时间与工作i的最早开始时间之差
E.工作j的最早开始时间与工作i的最迟完成时间之差
本题考查的是单代号网络计划时间参数的计算。(1)网络计划终点节点所代表的工作的总时差应等于计划工期与计算工期之差,即:TFn=T2020教材P-Tc;(2)当计划工期等于计算工期时,该工作的总时差为零。即TFn=T2020教材P-Tc=0;(3)其他工作的总时差应等于本工作与其各紧后工作之间的时间间隔加该紧后工作的总时差所得之和的最小值,即:TFi=min{LAGi,j+TFj}。
