判断题在XOY坐标系下,在[a,b]中曲线y=f(x)始终在曲线y=g(x)之上,则由它们所围平面区域的面积为:f(x)―g(x)在[a,b]上的定积分。A 对B 错
题目
判断题
在XOY坐标系下,在[a,b]中曲线y=f(x)始终在曲线y=g(x)之上,则由它们所围平面区域的面积为:f(x)―g(x)在[a,b]上的定积分。
A
对
B
错
参考答案和解析
正确答案:
错
解析:
暂无解析
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。
(1)求函数y=f(x);
(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
正确答案:
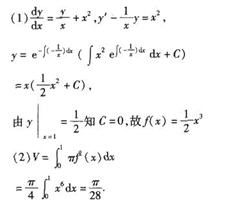
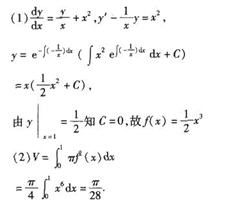
第2题:
在直角坐标系下,平面曲线f(x,y)=0可将平面分为( )个点集,当f(x,y) 大于0时,表示的点集为其正侧,至于是在曲线的外部还是内部则依赖于曲线的方向。
A. 1
B.2
C.3
D.4
参考答案:C
第3题:
设平面区域D由曲线y=1/x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
参考答案:

第4题:
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
答案:
解析: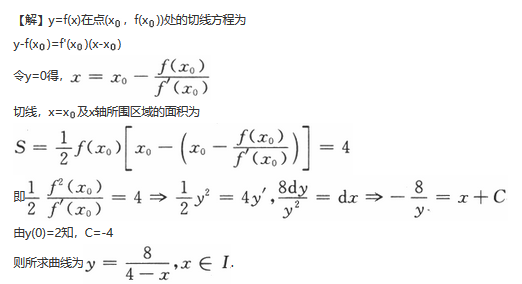
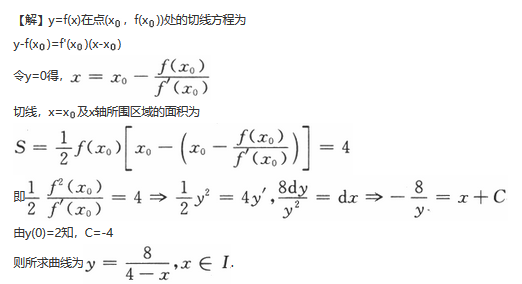
第5题:
设f(x)、g(x)在区间[a,b]上连续,且g(x)<f(x)<m(m为常数),由曲线y=g(x),y=f(x),x=a及x=b所围平面图形绕直线y=m旋转而成的旋转体体积为( )。
A.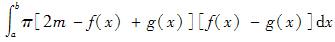
B.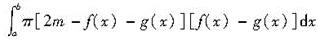
C.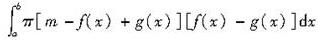
D.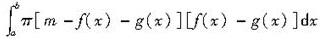
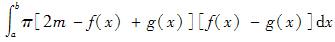
B.
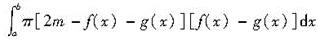
C.
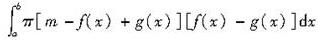
D.
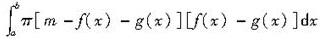
答案:B
解析: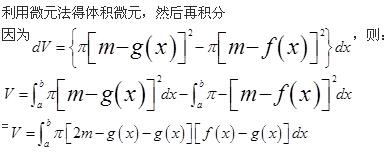
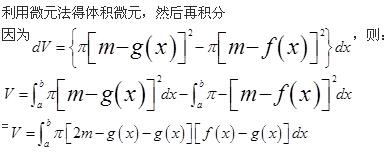
第6题:
由曲线y=x3,y=0,x=-1,x=l所围图形的面积为____。
正确答案:
1/2
1/2
第7题:
如果曲线y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( )。
A. y=x3-2
B. y=2x3-5
C. y=x2-2
D. y=2x2-5
正确答案:B
由曲线过点(1,-3)排除A、C项。由此曲线过点(2,11)排除D,故选B。y=2x3-5显然过点(1,-3)和(2,11),且它在(x,y)处的切线斜率为6x2,显然满足与x2成正比。
第8题:
在直角坐标系下,平面曲线f(x,y)=0可将平面分为___个点集,当f(x,y)大于0时,表示的点集为其正侧,至于是曲线的外部还是内部则依赖于曲线的方向。
A.1
B.2
C.3
D.4
参考答案:C
第9题:
求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.
答案:
解析:
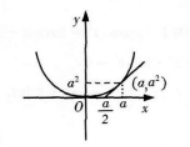
即y=2ax-a2,
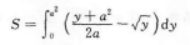
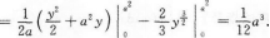


即y=2ax-a2,
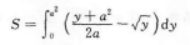
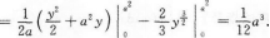
第10题:
设函数f(x)具有2阶连续导数,若曲线y=f(x)过点(0,0)且与曲线y=^x在点(1,2)处相切,则 =________.
=________.
 =________.
=________.答案:1、2(ln2-1)
解析:

