填空题在任意一次试验中，事件A服从0～1分布，那么在相同的条件下，进行n次独立、重复试验，用X表示这n次试验中事件A发生的次数，那么X服从（）。

由n次随机试验组成的随机现象，满足( )条件，称为二项分布。

A．重复进行几次随机试验

B．n次试验间相互独立，即每一次试验结果不对其他试验结果产生影响

C．每次试验仅有两个可能结果，例如，正面与反面，合格与不合格

D．每次试验成功的概率均为p，失败的概率均为1-P

E．只需进行一定量的试验次数即可

概率的统计定义的要点为( )。

A．与事件A有关的随机现象是可以大量重复试验的

B．若在n次重复试验中，事件A发生k次，则事件A发生的频率为fn(A)=kn/n，频率 fn(A)能反映事件A发生的可能性的大小

C．频率fn(A)将会随着重复试验次数不断增加而趋于稳定，这个频率的稳定值就是事件A的概率

D．实际中人们无法把一个试验无限次的重复下去，只能用重复试验次数n较大时的频率去近似概率

E．只要概率统计工作做的精确，统计结果可以和事实完全相符

概率的统计定义的要点为（ ）。

A．与事件A有关的随机现象是可以大量重复实验的

B．若在n次重复实验中，事件A发生Kn次，则事件A发生的频率为fn(A)=Kn/n频率，“(A)能反映事件A发生的可能性的大小

C．频率发fn(A)将会随着重复实验次数不断增加而趋于稳定，这个频率的稳定值就是事件A的概率

D．实际中人们无法把一个试验无限次的重复下去，只能用重复试验次数n较大时的频率去近似概率

在n重贝努里试验中,若事件A在每次试验中发生的概率为p,试证明:对任意ε>0,事件A发生的频率A与事件un/n发生的概率p有如下关系: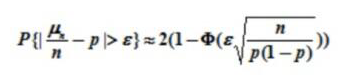

请帮忙给出正确答案和分析，谢谢!

在某事件的每次实验中，设成功的概率为P，则失败的概率为Q（＝1-P），在n次实验中，该事件成功k次的概率为Pn（k）＝CnkPk（1-P）n-k，问成功次数k服从什么分布

A、泊松分布

B、二项分布

C、正态分布

D、F分布

E、超儿何分布

小概率事件原理是( )。

A．小概率事件在一次试验中几乎不可能发生

B．小概率事件在一次试验中可能发生

C．小概率事件在一次试验中必然发生

D．小概率事件在一次试验中可能发生，可能不发生

A、1-Pn

B、Pn

C、1-(1-P)n

D、(1-P)n+nP(1-P)n-1