单选题设函数f(x)在区间[1,+∞)内二阶可导,且满足条件f(1)=f′(1)=0,x>1时f″(x)<0,则g(x)=f(x)/x在(1,+∞)内( )。A 曲线是向上凹的B 曲线是向上凸的C 单调减少D 单调增加
题目
单选题
设函数f(x)在区间[1,+∞)内二阶可导,且满足条件f(1)=f′(1)=0,x>1时f″(x)<0,则g(x)=f(x)/x在(1,+∞)内( )。
A
曲线是向上凹的
B
曲线是向上凸的
C
单调减少
D
单调增加
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设函数f(x)在点x=a处可导,则函数|f(x)|在点x=a处不可导的充分条件是( )
A.f(a)=0且f′(a)=0
B.f(a)=0且f′(a)≠0
C.f(a)>0且f′(a)>
D.f(a)<0且f′(a)<
B.f(a)=0且f′(a)≠0
C.f(a)>0且f′(a)>
D.f(a)<0且f′(a)<
答案:B
解析: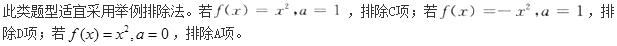
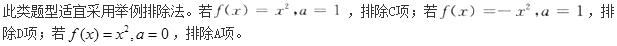
第2题:
设f(x)在闭区间[0,1]上连续,在(0,1)内可导,且f(0)=0,
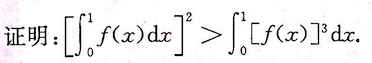

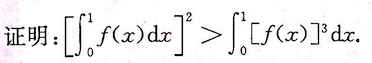
答案:
解析: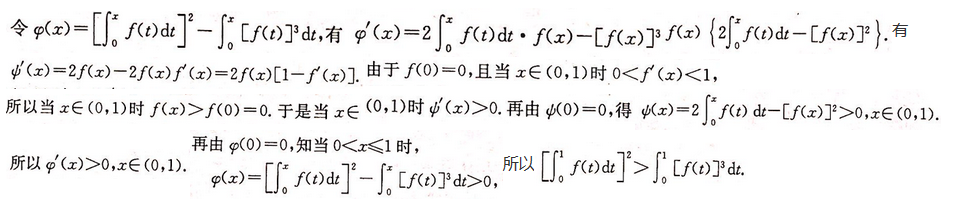
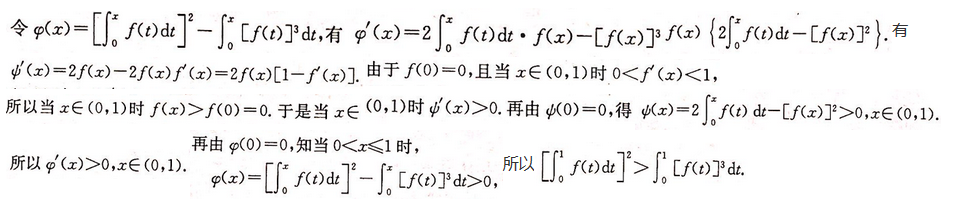
第3题:
设f(x)在[0,1]上可导,且满足f(1)=∫01xf(x)dx,证明:必有一点ξ∈(0,1),使得ξf(ξ)+f(ξ)=0.
第4题:
设函数f(x)具有二阶连续导数,且f(x)>0,f'(0)=0,则函数z=f(x)lnf(y)在点(0,0)处取得极小值的一个充分条件是
A.Af(0)>1,f"(0)>0
B.f(0)>1,f"(0)<0
C.f(0)<1,f"(0)>0
D.f(0)<1,f"(0)<0
B.f(0)>1,f"(0)<0
C.f(0)<1,f"(0)>0
D.f(0)<1,f"(0)<0
答案:A
解析:

第5题:
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
A.A当f'(x)≥0时,f(x)≥g(x)
B.当f'(x)≥0时,f(x)≤g(x)
C.当f"(x)≥0时,f(x)≥g(x)
D.当f"(x)≥0时,f(x)≤g(x)
B.当f'(x)≥0时,f(x)≤g(x)
C.当f"(x)≥0时,f(x)≥g(x)
D.当f"(x)≥0时,f(x)≤g(x)
答案:D
解析:
由于g(0)=f(0),g(1)=f(1),则直线y=f(0)(1-x)+f(1)x过点(0,f(0))和(1,f(1)),当f"(x)≥0时,曲线y=f(x)在区间[0,1]上是凹的,曲线y=f(x)应位于过两个端点(0,f(0))和(1,f(1))的弦y=f(0)(1-x)+f(1)x的下方,即f(x)≤g(x)故应选(D).
(方法二)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F'(x)=f'(x)+f(0)-f(1),F"(x)=f"(x).当f"(x)≥0时,F"(x)≥0,则曲线y=F(x)在区间[0,1]上是凹的.又F(0)=F(1)=0,从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).
(方法三)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F(x)=f(x)[(1-x)+x]-f(0)(1-x)-f(1)x
=(1-x)[f(x)-f(0)]-x[f(1)-f(x)]
=x(1-x)f'(ξ)-x(1-x)f'(η) (ξ∈(0,x),η∈(x,1))
=x(1-x)[f'(ξ)-f'(η)]
当f"(x)≥0时,f'(x)单调增,f'(ξ)≤f'(η),从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).
(方法二)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F'(x)=f'(x)+f(0)-f(1),F"(x)=f"(x).当f"(x)≥0时,F"(x)≥0,则曲线y=F(x)在区间[0,1]上是凹的.又F(0)=F(1)=0,从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).
(方法三)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F(x)=f(x)[(1-x)+x]-f(0)(1-x)-f(1)x
=(1-x)[f(x)-f(0)]-x[f(1)-f(x)]
=x(1-x)f'(ξ)-x(1-x)f'(η) (ξ∈(0,x),η∈(x,1))
=x(1-x)[f'(ξ)-f'(η)]
当f"(x)≥0时,f'(x)单调增,f'(ξ)≤f'(η),从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).
第6题:
设函数f(x)在x=1处可导,且f'(1)=0,若f"(1)>0,则f(1)是()
A.极大值
B.极小值
C.不是极值
D.是拐点
B.极小值
C.不是极值
D.是拐点
答案:B
解析:
由极值的第二充分条件可知,应选B.
第7题:
设f(x)二阶可导,f(0)= f(1),且f(x)在[0,1]上的最小值为—1.证明:

答案:
解析:

第8题:
设函数f(x)与g(x)在[0,1]上连续,且f(x)≤g(x),且对任何的c∈(0,1)( )
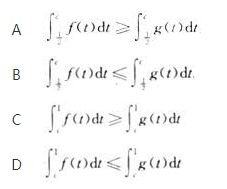
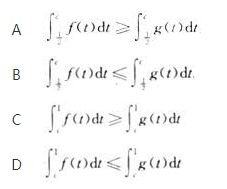
答案:D
解析: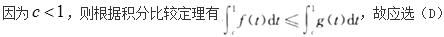
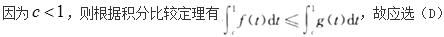
第9题:
设函数f(x)可导,且f(x)f'(x)>0,则
A.Af(1)>f(-1)
B.f(1)
D.|f(1)|<|f|(-1)|
B.f(1)
D.|f(1)|<|f|(-1)|
答案:C
解析:

第10题:
设f(x)是周期为4的可导奇函数,且f'(x)=2(x-1),x∈[0,2],则f(7)=________.
答案:1、1.
解析:
由f'(x)=2(x-1),x∈[0,2]知,f(x)=(x-1)^2+C.又f(x)为奇函数,则f(0)=0,C=-1.f(x)=(x-1)^2-1.由于f(x)以4为周期,则f(7)=f[8+(-1)]=f(-1)=-f(1)=1.
