单选题设λ1,λ2是矩阵A的2个不同的特征值,ξ,η是A的分别属于λ1,λ2的特征向量,则以下选项中正确的是:()A 对任意的k1≠0和k2≠0,k1ξ+k2η,都是A的特征向量B 存在常数k1≠0和k2≠0,使得k1ξ+k2η,是A的特征向量C 存在任意的k1≠0和k2≠0,k1ξ+k2η,都不是A的特征向量D 仅当k1=k2=0时,k1ξ+k2η,是A的特征向量
题目
单选题
设λ1,λ2是矩阵A的2个不同的特征值,ξ,η是A的分别属于λ1,λ2的特征向量,则以下选项中正确的是:()
A
对任意的k1≠0和k2≠0,k1ξ+k2η,都是A的特征向量
B
存在常数k1≠0和k2≠0,使得k1ξ+k2η,是A的特征向量
C
存在任意的k1≠0和k2≠0,k1ξ+k2η,都不是A的特征向量
D
仅当k1=k2=0时,k1ξ+k2η,是A的特征向量
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
已知二阶实对称矩阵A的特征值是1,A的对应于特征值1的特征向量为(1,-1)T,若|A|=-1,则A的另一个特征值及其对应的特征向量是( )。
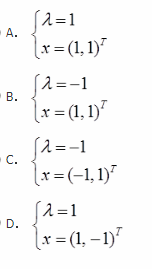
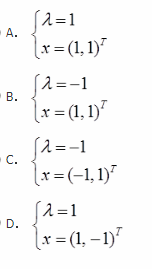
答案:B
解析:
根据矩阵行列式与特征值的关系:|A|=λ1λ2,故另一个特征值为-1,其对应的特征向量应与已知特征向量正交,即两向量点乘等于零,因此(1,1)T满足要求。
第2题:
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
A. Pa B. P-1
A. Pa B. P-1
A C. PTa D.(P-1)Ta
答案:B
解析:

第3题:
设λ1</sub>,λ2</sub>都是n阶矩阵A的特征值,λ1</sub>≠λ2</sub>,,且a1</sub>与a2</sub>分别是A的对应于λ1</sub>与λ2</sub>的特征向量,则().
A.c1=0且c2=0时,a=c1a1+c2a2必是A的特征向量
B.c1≠0且c2≠0时,a=c1a1+c2a2必是A的特征向量
C.c1,c2=0时,a1=c1a1+c2a2必是A的特征向量
D.c1≠0而c2=0时,a=c1a1+c2a2必是A的特征向量
参考答案:

第4题:
设A是三阶实对称矩阵,r(A)=1,A^2-3A=O,设(1,1,-1)t为A的非零特征值对应的特征向量.(1)求A的特征值;(2)求矩阵A.
答案:
解析:

第5题:
设λ1,λ2是矩阵A 的2 个不同的特征值,ξ,η 是A 的分别属于λ1,λ2的特征向量,
则以下选项中正确的是:
(A)对任意的k1≠ 0和k2 ≠0,k1 ξ+k2η 都是A 的特征向量
(B)存在常数k1≠ 0和k2≠0,使得k1ξ+k2η 是A 的特征向量
(C)存在任意的k1≠ 0和k2≠ 0, k1ξ+ k2η 都不是A 的特征向量
(D)仅当k1=k2=时, k1ξ+k2 η 是A 的特征向量
则以下选项中正确的是:
(A)对任意的k1≠ 0和k2 ≠0,k1 ξ+k2η 都是A 的特征向量
(B)存在常数k1≠ 0和k2≠0,使得k1ξ+k2η 是A 的特征向量
(C)存在任意的k1≠ 0和k2≠ 0, k1ξ+ k2η 都不是A 的特征向量
(D)仅当k1=k2=时, k1ξ+k2 η 是A 的特征向量
答案:C
解析:
解:选C。
特征向量必须是非零向量,所以选项(D)错误。
由于“对应于不同特征值的特征向量必定线性无关”,因此ξ,η 线性无关,即k1ξ+k2η = 0
仅当k1=k2=时才成立。
特征向量必须是非零向量,所以选项(D)错误。
由于“对应于不同特征值的特征向量必定线性无关”,因此ξ,η 线性无关,即k1ξ+k2η = 0
仅当k1=k2=时才成立。
第6题:
设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().
A.矩阵A不可逆
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量
答案:C
解析:
由λ1=-1,λ2=0,λ3=1得|A|=0,则r(A)小于3,即A不可逆,(A)正确;又λ1+λ2+λ3=tr(A)=0,所以(B)正确;因为A的三个特征值都为单值,所以A的非零特征值的个数与矩阵A的秩相等,即r(A)=2,从而AX=0的基础解系仅含有一个线性无关的解向量,(D)是正确的;(C)不对,因为只有实对称矩阵的不同特征值对应的特征向量正交,一般矩阵不一定有此性质,所以选(C).
第7题:
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:(A) Pα (B) P-1α (C) PTa (D) P(-1)Ta
答案:A
解析:
解:选A。
考察了实对称矩阵的特点,将选项分别代入检验可得到答案。
考察了实对称矩阵的特点,将选项分别代入检验可得到答案。
第8题:
n*n矩阵可看作是n维空间中的线性变换,矩阵的特征向量经过线性变换后,只是乘以某个常数(特征值),因此,特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1,w2,w3),其对应的特征值为( )。

A.1/3
B.1
C.3
D.9
正确答案:C
解析:n*n矩阵可看做是n维空间中的线性变换,它将任何一个向量x变换成新的向量(A的矩阵与列向量x的乘积)。三维空间中的旋转变换就是一种线性变换,它将一个变量变换成另一个变量。旋转变换必然绕某个轴旋转,这个轴上的向量经过该旋转变换后得到的向量仍会保持在这根轴上。这根轴上的向量属于该旋转变换的特征向量。对于单纯的旋转变换来说,这根旋转轴上的特征向量所对应的特征值为1。线性变换A的特征向量Y及其相应的特征值λ满足AY=λY,其几何意义是特征向量Y经过线性变换A变换成向量λY(保持在同一轴上,只是乘以常数λ,放大或缩小入倍,λ为负时变为相反方向)。本题中的矩阵A以及由w1、w2、w3组成的列向量w具有关系(可以通过矩阵乘法得到)Aw=3w,所以,(w1、w2、w3)是该矩阵的特征向量,其相应的特征值为3。
解析:n*n矩阵可看做是n维空间中的线性变换,它将任何一个向量x变换成新的向量(A的矩阵与列向量x的乘积)。三维空间中的旋转变换就是一种线性变换,它将一个变量变换成另一个变量。旋转变换必然绕某个轴旋转,这个轴上的向量经过该旋转变换后得到的向量仍会保持在这根轴上。这根轴上的向量属于该旋转变换的特征向量。对于单纯的旋转变换来说,这根旋转轴上的特征向量所对应的特征值为1。线性变换A的特征向量Y及其相应的特征值λ满足AY=λY,其几何意义是特征向量Y经过线性变换A变换成向量λY(保持在同一轴上,只是乘以常数λ,放大或缩小入倍,λ为负时变为相反方向)。本题中的矩阵A以及由w1、w2、w3组成的列向量w具有关系(可以通过矩阵乘法得到)Aw=3w,所以,(w1、w2、w3)是该矩阵的特征向量,其相应的特征值为3。
第9题:
设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,
对应特征向量为(-1,0,1)^T.
(1)求A的其他特征值与特征向量;
(2)求A.
对应特征向量为(-1,0,1)^T.
(1)求A的其他特征值与特征向量;
(2)求A.
答案:
解析:

第10题:
设A是n阶矩阵,λ是A的特征值,其对应的特征向量为X,证明:λ^2是λ^3的特征值,X为特征向量,若A^2有特征值λ,其对应的特征向量为X,X是否一定为A的特征向量?说明理由.
答案:
解析:

