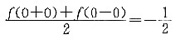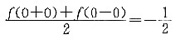填空题复杂的周期信号可借助傅里叶级数展开成(),其中任两个分量的频率比都是有理数.
题目
填空题
复杂的周期信号可借助傅里叶级数展开成(),其中任两个分量的频率比都是有理数.
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
傅里叶级数中的系数表示谐波分量的( )。
A: 相位
B: 周期
C: 振幅
D: 频率
正确答案: C
第2题:
一般周期信号可以利用傅里叶级数展开成()不同频率的谐波信号的线性叠加。
A、两个
B、多个乃至无穷多个
C、偶数个
D、奇数个
参考答案:B
第3题:
周期连续信号的频率描述应用()对信号进行分解。
A、拉式变换
B、傅里叶变换
C、相关函数
D、傅里叶级数
参考答案:D
第4题:
设f(x)是周期为2π的周期函数,它在[-π,π]上的表达式为:
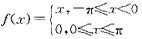
若将f(x)展开成傅里叶级数,则该级数在x=-3π处收敛于( )。

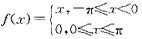
若将f(x)展开成傅里叶级数,则该级数在x=-3π处收敛于( )。

答案:C
解析:
所给函数满足收敛定理,当x=-3π为函数的问断点,函数f(x)的傅里叶级数在x
第5题:
已知f(t)是周期为T的函数,f(t)-f(t+(5/2)T)的傅里叶级数中,不可能的是()。
A、正弦分量
B、余弦分量
C、奇次谐波分量
D、偶次谐波分量
参考答案:ABD
第6题:
非正弦周期电流电路稳态分析有2个步骤展开成傅里叶级数和叠加出最后结果。()
正确答案:错误
第7题:
傅里叶级数展开中,包含正弦分量,则原信号必为奇函数。()
此题为判断题(对,错)。
参考答案:错误
第8题:
非正弦周期信号的分解可用什么方法实现:()
A.傅里叶变化;
B.傅里叶变换;
C.傅里叶级数展开;
D.傅里叶卷积
正确答案:A
第9题:
若周期信号f(t)是时间t的奇函数,则其三角形傅里叶级数展开式中()。
A.没有余弦分量
B.既有正弦分量和余弦分量,又有直流分量
C.既有正弦分量和余弦分量
D.仅有正弦分量
正确答案:D
第10题:
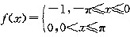
展开成傅里叶级数时,该级数在x=0处的值为( )。

答案:B
解析:
x=0是f(x)的第一类间断点,根据收敛定理,级数在点x=0处收敛于