问答题设A=E-ααT,其中E是n阶单位矩阵,α是n维非零列向量,αT是α的转置.证明:(1)A2=A的充要条件是αTα=1;(2)当αTα=1时,A是不可逆矩阵.
题目
问答题
设A=E-ααT,其中E是n阶单位矩阵,α是n维非零列向量,αT是α的转置.证明:(1)A2=A的充要条件是αTα=1;(2)当αTα=1时,A是不可逆矩阵.
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设A、B都是n阶可逆矩阵,则
A. (-3)n A B -1
B. -3 A T B T
C. -3 A T B -1
D. (-3)2n A B -1

A. (-3)n A B -1
B. -3 A T B T
C. -3 A T B -1
D. (-3)2n A B -1
答案:D
解析:

第2题:
设A为m阶实对称矩阵且正定,B为m×n实矩阵,B^T为B的转置矩阵,试证:B^TAB为正定矩阵的充分必要条件是B的秩r(B)=n,
答案:
解析:

第3题:
●已知有二维数组A[0..n-1][0..n-1],其中当i+j=n时,A[i][j]≠0,现在要将A数组压缩存储到一维数组T[0..m],其中m>n。数组T的第一个元素T[0]=A[1][n-1] T[1]=A[2][n-2],……,依次类推,那么放入A[i][j](i+j=n)的元素是 (37) 。
(37) A.T[i+j]
B.T[i*n+j]
C.T[i]
D.T[i-1]
正确答案:D
【解析】由题可知,除第0行外,每一行只存储一个元素,因此i行应存放在T[i-1]之中。
【解析】由题可知,除第0行外,每一行只存储一个元素,因此i行应存放在T[i-1]之中。
第4题:
设α为n维单位列向量,E为n阶单位矩阵,则
A.AE-AA^T不可逆
B.E+AA^T不可逆
C.E+2AA^T不可逆
D.E-2AA^T不可逆
B.E+AA^T不可逆
C.E+2AA^T不可逆
D.E-2AA^T不可逆
答案:A
解析:
A=αα^T是秩为1的矩阵,又α为单位列向量,有α^Tα=1.故矩阵A的特征值为1,0,…,0(n-1个)所以E-αα^T的特征值为0,1,…,1(n-1个)因此矩阵E-αα^T不可逆.应选(A)
第5题:
设A是三阶实对称矩阵,r(A)=1,A^2-3A=O,设(1,1,-1)t为A的非零特征值对应的特征向量.(1)求A的特征值;(2)求矩阵A.
答案:
解析:

第6题:
设A为n阶矩阵,证明:r(A)=1的充分必要条件是存在n维非零列向量α,β使得A=αβT.
答案:
解析:

第7题:
设非零n维列向量α,β正交且A=αβT.证明:A不可以相似对角化.
答案:
解析:

第8题:
已知有二维数组A[0..n-1][0..n-1],其中当i+j=n时,A[i][j]≠0,现在要将A数组压缩存储到一维数组T[0..m],其中m>n。数组T的第一个元素T[0]=A[1][n-1] T[1]=A[2][n-2],……,依次类推,那么放入A[i][j](i+j=n)的元素是(37)。
A.T[i+j]
B.T[i*n+j]
C.T[i]
D.T[i-1]
正确答案:D
解析:由题可知,除第0行外,每一行只存储一个元素,因此i行应存放在T[i-1]之中。
解析:由题可知,除第0行外,每一行只存储一个元素,因此i行应存放在T[i-1]之中。
第9题:
设α,β为三维列向量,矩阵A=αα^T+ββ^T,其中α^T,β^T分别是α,β的转置.证明:
(Ⅰ)秩r(A)≤2;
(Ⅱ)若α,β线性相关,则秩r(A)<2.
(Ⅰ)秩r(A)≤2;
(Ⅱ)若α,β线性相关,则秩r(A)<2.
答案:
解析:
【证明】(Ⅰ)因为α,β为三维列向量,那么αα^T和ββ^T都是三阶矩阵,
且秩r(αα^T)≤1,r(ββ^T)≤1.
那么,r(A)=r(αα^T+ββ^T)≤r(αα^T)+r(ββ^T)≤2.
(Ⅱ)由于α,β线性相关,不妨设α=kβ,于是
r(A)=r(αα^T+ββ^T)=r((1+k^2)ββ^T)≤r(β)≤1<2.
【评注】本题考查矩阵秩的性质公式.
(Ⅰ)中有两个基本知识点:①r(αα^T)≤1和②r(A+B)≤r(A)+r(B).
(Ⅱ)中有两个基本知识点:①α,β线性相关的几何意义和②r(kA)=r(A),k≠0.
注意,如果分块矩阵比较熟悉,本题的(Ⅰ)也可如下处理:
因为
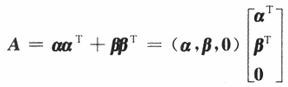
那么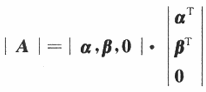
从而r(A)≤2.
且秩r(αα^T)≤1,r(ββ^T)≤1.
那么,r(A)=r(αα^T+ββ^T)≤r(αα^T)+r(ββ^T)≤2.
(Ⅱ)由于α,β线性相关,不妨设α=kβ,于是
r(A)=r(αα^T+ββ^T)=r((1+k^2)ββ^T)≤r(β)≤1<2.
【评注】本题考查矩阵秩的性质公式.
(Ⅰ)中有两个基本知识点:①r(αα^T)≤1和②r(A+B)≤r(A)+r(B).
(Ⅱ)中有两个基本知识点:①α,β线性相关的几何意义和②r(kA)=r(A),k≠0.
注意,如果分块矩阵比较熟悉,本题的(Ⅰ)也可如下处理:
因为
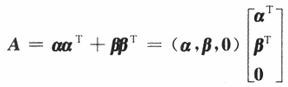
那么
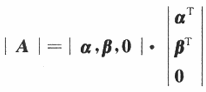
从而r(A)≤2.
第10题:
设α为三维单位列向量,E为三阶单位矩阵,则矩阵E-αα^T的秩为________.
答案:
解析:

