数学
填空题已知随机变量X～N（－1，1），Y～N（3，1），且X、Y相互独立，Z＝X－2Y，则Z～____。
题目
填空题
已知随机变量X～N（－1，1），Y～N（3，1），且X、Y相互独立，Z＝X－2Y，则Z～____。
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设随机变量X,Y,Z相互独立,且X～U［-1,3］,Y～B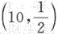
,Z～N(1,3……2),且随机变量U=X+2Y-32+2,则D(U)=_______.
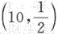,Z～N(1,3……2),且随机变量U=X+2Y-32+2,则D(U)=_______.答案：
解析：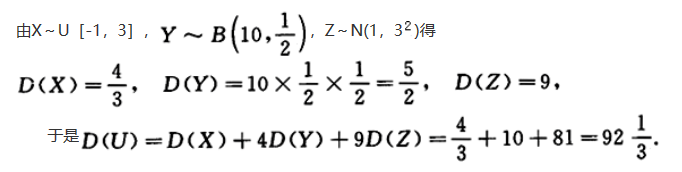
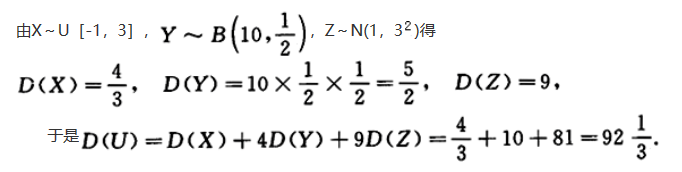
第2题：
设随机变量X,Y相互独立,且X～N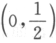
,Y～N
,Z=｜X-Y｜,求
E(Z),D(Z).
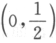,Y～N,Z=｜X-Y｜,求
E(Z),D(Z).
答案：
解析：
第3题：
设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()
参考答案：97
第4题：
设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=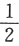
.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为
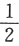.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为 A.A0
B.1
C.2
D.3
B.1
C.2
D.3
答案：D
解析：
第5题：
设随机变量X,Y相互独立,且X～N(0,4),Y的分布律为Y～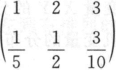
.则P(X-1-2Y≤4)=_______.
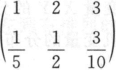.则P(X-1-2Y≤4)=_______.答案：1、0.46587
解析：
p(X+2Y≤4)=P(Y=1)P(X≤4-2Y｜Y=1)+P(Y=2)P(X≤4-2Y｜Y=2)+P(Y=3)P(X≤4-2Y｜Y=3)
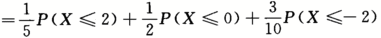
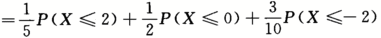
第6题：
设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相
关系数为－
,又设Z=
(1)求E(Z),D(Z)；(2)求
；(3)X,Z是否相互独立？为什么？
关系数为－
,又设Z=
(1)求E(Z),D(Z)；(2)求
；(3)X,Z是否相互独立？为什么？答案：
解析：
【解】(1)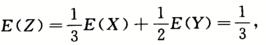
(2)
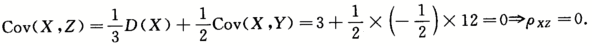
(3)因为(X，Y)服从二维正态分布，所以Z服从正态分布，同时X也服从正态分布，又X，
Z不相关，所以X，Z相互独立.
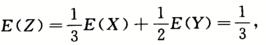
(2)
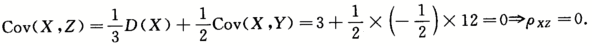
(3)因为(X，Y)服从二维正态分布，所以Z服从正态分布，同时X也服从正态分布，又X，
Z不相关，所以X，Z相互独立.
第7题：
设随机变量X～N(μ,σ^2),Y～U［－π,π］,X,Y相互独立,令Z=X+Y,求fz(z).
答案：
解析：
第8题：
设 X、Y相互独立，X~N(4，1),Y~N(1，4),Z=2X-Y，则
A.0 B.8 C. 15 D. 16
A.0 B.8 C. 15 D. 16
答案：B
解析：
提示：由方差性质D(Z) =D(2X)+D(Y) = 4D(X)+D(Y) = 4x1 + 4。
第9题：
设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.
答案：
解析：
由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且
，故
.
，故.第10题：
设随机变量X,Y相互独立,且X～N(0,1),Y～N(1,1),则().
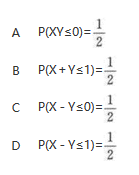
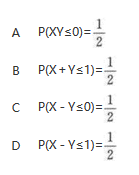
答案：B
解析：
X，Y独立，X～N(0，1)，Y～N(1，1)，X+Y～N(1，2)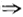
P(X+Y≤1)=
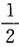，所以选(B).
P(X+Y≤1)=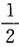，所以选(B).