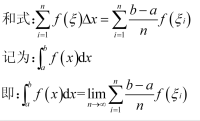请教:2009年江苏省某市教师公开招聘考试《小学数学》试卷第4大题第7小题如何解答?【题目描述】五、应用题(本大题共3小题,共25分)第 18 题某团体从甲地到乙地,甲、乙两地相距100千米,团体中一部分人乘车先行,余下的人步行,先坐车的人到途中某处下车步行,汽车返回接先步行的那部分人,已知步行速度为8千米/4,时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?(8分)
题目
【题目描述】
五、应用题(本大题共3小题,共25分)
第 18 题某团体从甲地到乙地,甲、乙两地相距100千米,团体中一部分人乘车先行,余下的人步行,先坐车的人到途中某处下车步行,汽车返回接先步行的那部分人,已知步行速度为8千米/4,时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?(8分)
相似问题和答案
第1题:
【题目描述】
第 72 题 甲、乙两地相距8千米,小玉每天从甲地骑自行车去乙地上班,以20千米/时的速度骑行,恰好准时到公司。一天,因为逆风,她提前0.4小时出发,以10千米/时的速度骑行到距乙地4.8千米时接了个电话被催促,她不得不加快速度,结果比预计时间早到了6分钟。小玉受到催促后每小时骑行多少千米?( )
|
正确答案:D |
正常情况下需要8÷20=0.4(小时),即24分钟,以10千米/时的速度骑行了3.2千米,用了0.32小时,即19.2分钟。所以骑行4.8千米共用了24—19.2+24—6=22.8(分钟),所以后来的速度为4.8÷(22.8÷60)≈12.6(千米/小时)。故本题正确答案为D。
第2题:
甲、已两地相距42公里,A、B两人分别同时从甲乙两地步行出发,A的步行速度为3公里/小时,B的步行速度为 4公里/小时,问A、B步行几小时后相遇?
A.3 B.4 C.5 D.6
【正确答案】D
【点拨】从一个终点站到另一个终点站用1小时,这样樊政在刚刚出发后看到的第一辆车应该是将近1小时前,另一个终点发出的车,而樊政在快到另一个终点时看到的最后一辆车,应该是在樊政出发后将近1小时后发车的。这样,樊政看到第一辆与最后一辆的发车时间的差应该是将近2小时,2小时中发出21辆车,说明正好每6分钟发一辆车。故应选择D选项。
第3题:
五、应用题(本大题共3小题,共25分)
第 18 题 某团体从甲地到乙地,甲、乙两地相距100千米,团体中一部分人乘车先行,余下的人步行,先坐车的人到途中某处下车步行,汽车返回接先步行的那部分人,已知步行速度为8千米/4,时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?(8分)

第4题:
【题目描述】
第 23 题

【参考答案分析】:
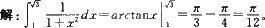
这个题目所求是一般的定积分,设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n个子区间[a,x0],(x0,x1], (x1,x2],…,(xi,b].在每个子区间(xi-1,xi)任取一点ξi(i=1,2,…,n),作和式(见右下图),当λ→0时,(λ属于最大的区间长度)该和式无限接近于某个常数,这个常数叫做函数f(x) 在区间(a,b)的定积分,记为(见右下图):
之所以称其为定积分,是因为它积分后得出的值是确定的,是一个数, 而不是一个函数。
第5题:
【题目描述】
第 49 题
 ( )
( )
|
正确答案:B |
答案分析:
a b c d e f g h i j k l m n o
注意看红色标记的地方,a 和 c之间相隔一个字母,c和f之间相隔2个字母,f和j之间相隔3个字母,那下一个就会隔4个字母,所以答案是O
第6题:
:某团体从甲地到乙地,甲、乙两地相距l00千米,团体中一部分人乘车先行,余下的人步行,先坐车的人到途中某处下车步行,汽车返回接先步行的那部分人,已知步行速度为8千米/小时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?( )
A.5.5小时
B.5小时
C.4.5小时
D.4小时

第7题:
【题目描述】
第 8 题课程标准实验教材与原教材的主要区别何在?试结合已有的教学经验,谈谈新教材的功能。
第8题:
【题目描述】
第 7 题

正确答案:B
原式等于(a2-b2)/a-b 即【(a-b)(a+b)】/(a-b) 化简约去a-b,即a+b
{(a-b)×(a+b)} ÷(a-b)=a+b
第9题:
:甲、乙两地相距42公里,A、B两人分别同时从甲乙两地步行出发,相向而行,A的步行速度为3公里/小时,8的步行速度为4公里/小时,问A、B步行几小时后相遇?( )
A.3
B.4
C.5
D.6
第10题:
【题目描述】
第 29 题甲、乙两港相距720千米,轮船往返两港需要35小时,逆流航行比顺流航行多花5小时,帆船在静水中每小时行驶24千米,问帆船往返两港需要多少小时?
参考答案分析】: