图所示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)
题目
图所示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)




如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
图所示的刚架,EI=常数,各杆长为l,A截面的转角为( )。
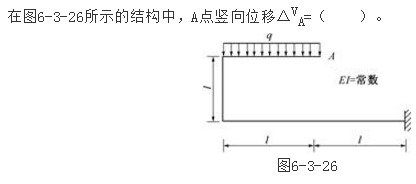
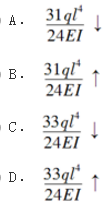

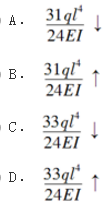
答案:A
解析: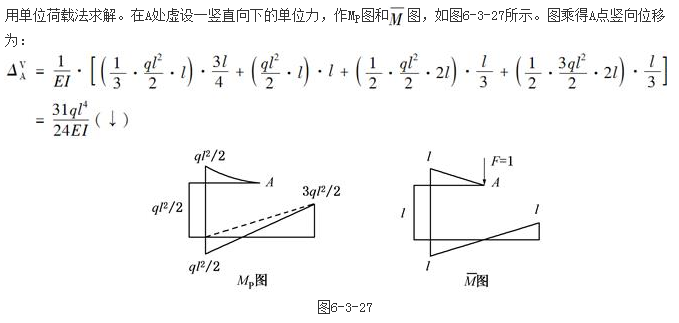

第2题:
已知刚架的弯矩图如图所示,杆的抗弯刚度为杆的为2EI,则结点B的角位移等于:




答案:C
解析:
提示:使用BA杆的转角位移方程。
第3题:
有如图所示简支梁,其抗弯刚度EI为常数。该梁的挠曲线方程为()。
A.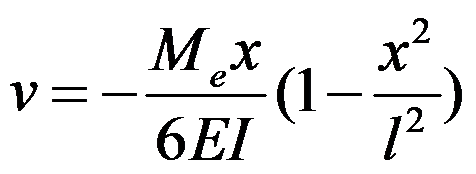
B.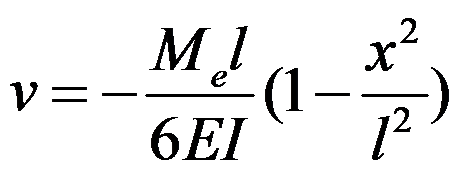
C.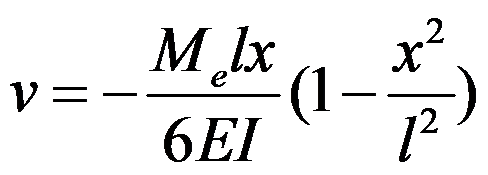
D.
答案:A
第4题:
图示梁AB,EI为常数,固支端A发生顺时针的支座转动,由此引起的B处的转角为( )。
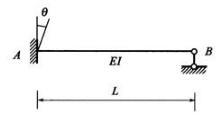



答案:D
解析:

第5题:
图所示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
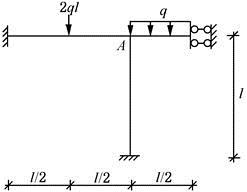



答案:D
解析:
在A点施加刚臂,并取出节点A分析,在单位转角下,其节点弯矩图如图所示。则刚度系数为k=4i+4i+2i=10i,i=EI/l。A点加刚臂后的节点荷载图如图所示。则A节点的总弯


第6题:
如图所示结构,EI为常数,欲使结点B的转角为零,则q的值为( )kN/m。
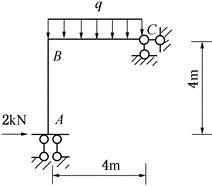

A、0
B、2
C、4
D、8
B、2
C、4
D、8
答案:B
解析:
在结点B处附加刚臂,得到位移法基本体系,建立位移法基本方程得:k11Δ1+F1P=0,由于结点B的转角Δ1为零,所以
{图}
解得q=2kN/m。
{图}
解得q=2kN/m。
第7题:
图示刚架,各杆线刚度相同,则结点A的转角大小为( )。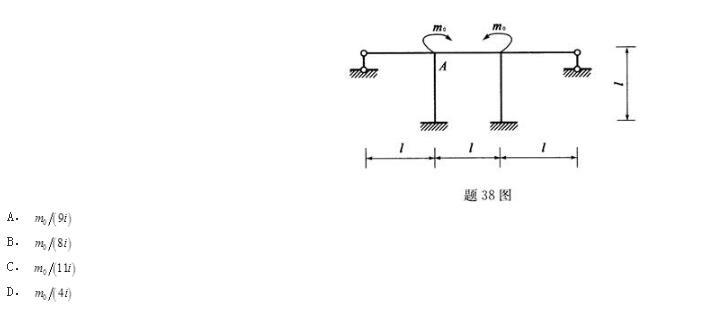

答案:A
解析:

第8题:
图所示刚架,各杆线刚度相同,则结点A的转角大小为( )。
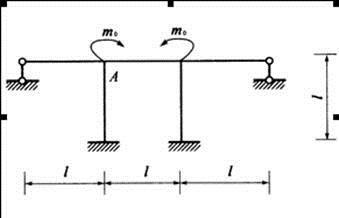



答案:A
解析:
利用对称性,取对称结构如下,应用位移法,在结点A加一个刚性支座。则结构中只有一个未知的角位移。截取结点A,得:
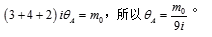
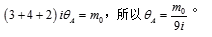
第9题:
图所示连续梁,EI为常数,用力矩分配法求得结点B的不平衡力矩为( )。


A、-20kN·m
B、15kN·m
C、-5kN·m
D、5kN·m
B、15kN·m
C、-5kN·m
D、5kN·m
答案:D
解析:
根据力矩分配法知,传递弯矩是分配弯矩乘以传递系数。不平衡力矩是指固端弯矩的代数和,则


第10题:
图示刚架EI=常数,结点B的水平位移为( )。


答案:D
解析:

