数学
设随机变量X的概率分布为P{X=k}=θ（1-θ）k-1，k=1，2，L，其中0<θ<1，若P{X≤2}=5/9，则P{X=3}=（）。
题目
设随机变量X的概率分布为P{X=k}=θ（1-θ）k-1，k=1，2，L，其中0<θ<1，若P{X≤2}=5/9，则P{X=3}=（）。
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
离散型随机变量X的分布为为P(X=k)=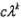
,(k=0,1,2...),则不成立的是：
(A) c＞0(B)0＜λ＜1 (C)c=1-λ (D)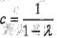
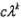,(k=0,1,2...),则不成立的是：
(A) c＞0(B)0＜λ＜1 (C)c=1-λ (D)
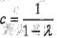
答案：D
解析：
因为概率总非负，所以cλk≥0 ，所以c≥0，但是如果c = 0，则
P（X = 0) + P(X = 1) + P(X = 2) +.. = 0 ≠ 1，显然不对，因此c ≠ 0，得c ＞ 0。
P( X = 0) + P( X = 1) + P( X = 2) +.. = c(1 + λ + λ2 +..）=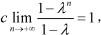
则0＜λ＜1，上式变为
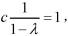得c=1-λ,所以选项（B）、(C)正确，（D）错误。
点评：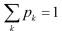
P（X = 0) + P(X = 1) + P(X = 2) +.. = 0 ≠ 1，显然不对，因此c ≠ 0，得c ＞ 0。
P( X = 0) + P( X = 1) + P( X = 2) +.. = c(1 + λ + λ2 +..）=
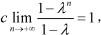则0＜λ＜1，上式变为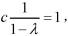得c=1-λ,所以选项（B）、(C)正确，（D）错误。
点评：
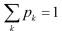
第2题：
设随机变量X服从参数为λ的泊松分布,且P（X=O）=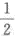
P（X=1）,则P(X≥1)=_______.
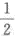P（X=1）,则P(X≥1)=_______.答案：
解析：
第3题：
随机变量X的概率分布表如下：
K
1
4
10
P
20%
40%
40%
则随机变量x的期望是（ ）。
A．5.8
B．5.6
C．4.5
D．4.8
正确答案：A
E（X）=1×20%+4×40%+10×40=5.8
E（X）=1×20%+4×40%+10×40=5.8
第4题：
设随机变量X的概率分布为P{X=1}=P{X=2}=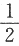
，在给定X=i的条件下，随机变量Y服从均匀分布U(0，i)(i=1，2).
(Ⅰ)求Y的分布函数FY(y)；
(Ⅱ)求EY.
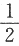，在给定X=i的条件下，随机变量Y服从均匀分布U(0，i)(i=1，2).
(Ⅰ)求Y的分布函数FY(y)；
(Ⅱ)求EY.
答案：
解析：
第5题：
设随机变量X和Y的联合分布是正方形G={(x，y)|1≤x≤3，1≤y≤3}上的均匀分布，试求随机变量U=|X-Y|的概率密度p(u).
答案：
解析：
本题是2001年数三的考题，考查两个随机变量函数的分布和均匀分布.
第6题：
设随机变量X与Y独立，其中X的概率分布为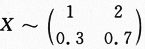
而Y的概率密度为f(y)，求随机变量U=X+Y的概率密度g(u).
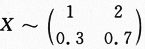而Y的概率密度为f(y)，求随机变量U=X+Y的概率密度g(u).答案：
解析：
【简解】本题是2003年数三的考题，考查一个离散型和一个连续型两个随机变量的函数的分布，随机变量的独立性等，
先求分布函数
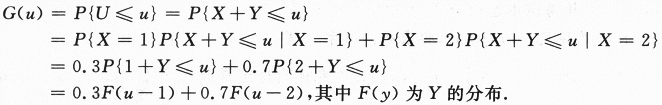
由此得g(u)=0.3f(u-1)+0.7f(u-2).
先求分布函数
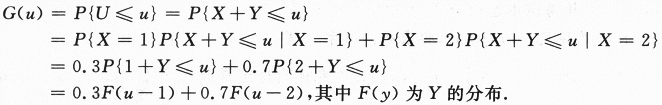
由此得g(u)=0.3f(u-1)+0.7f(u-2).
第7题：
设随机变量X在区间(0，1)内服从均匀分布，在X=x(0
(Ⅱ)Y的概率密度；
(Ⅲ)概率P{X+Y>1}.
(Ⅱ)Y的概率密度；
(Ⅲ)概率P{X+Y>1}.
答案：
解析：
【简解】本题是数四2004年考题，考查均匀分布，二维随机变量的概率密度、边缘密度和条件密度，当年的得分率仅为0.204.主要的困难在于对条件概率密度的理解.
第8题：
设随机变量X的分布函数为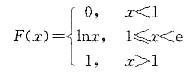 
则X的概率密度函数f(x)为( )。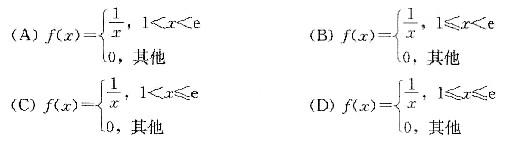 
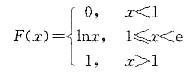则X的概率密度函数f(x)为( )。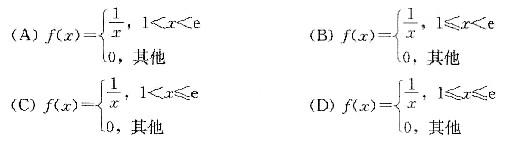 答案：B
解析：
由分布函数与概率密度函数关系f(x)=F'(x)，当1≤x＜e时，f(x)=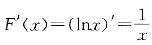
，X的概率密度综合表示为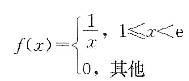
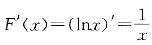，X的概率密度综合表示为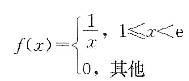第9题：
设二维离散型随机变量(X，Y)的概率分布为
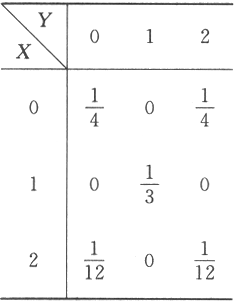
(Ⅰ)求P{X=2Y)；
(Ⅱ)求Cov(X-Y，Y).
(Ⅰ)求P{X=2Y)；
(Ⅱ)求Cov(X-Y，Y).
答案：
解析：
第10题：
设随机变量X与Y的概率分布分别为
，
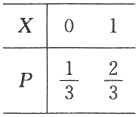且P{X^2=Y^2}=1.
(Ⅰ)求二维随机变量(X，Y)的概率分布；
(Ⅱ)求Z=XY的概率分布；
(Ⅲ)求X与Y的相关系数ρXY.
，
且P{X^2=Y^2}=1.
(Ⅰ)求二维随机变量(X，Y)的概率分布；
(Ⅱ)求Z=XY的概率分布；
(Ⅲ)求X与Y的相关系数ρXY.
答案：
解析：