设E、F点的纵坐标分别为300米和400米,则纵坐标增量△xFE为()。A、100米B、700米C、-100米D、-700米
题目
设E、F点的纵坐标分别为300米和400米,则纵坐标增量△xFE为()。
- A、100米
- B、700米
- C、-100米
- D、-700米
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
若B点的坐标为(500.000,500.000)m,BP平距、方位角分别为100.000m和60°00'00²,则P点的纵坐标()m。
A.450.000
B.500.000
C.550.000
D.586.603
答案:C
第2题:
对统计图中的的坐标有如下规定:
A、所有统计图的纵坐标都必须从零点开始
B、所有统计图坐标中都不能有折断线
C、条图、线图、直方图的纵坐标必须从零开始
D、线图、直方图的纵坐标必须从零开始
E、条图、直方图的纵坐标必须从零开始
参考答案:E
第3题:
挣值法评价曲线,坐标阐述正确的是()
A.横坐标表示时间,纵坐标则表示费用。
B.横坐标表示费用,纵坐标则表示时间。
C.横坐标表示进度,纵坐标则表示费用。
D.横坐标表示时间,纵坐标则表示进度。
正确答案:A
第4题:
1坐标正算中,下列何项表达了纵坐标增量?( )
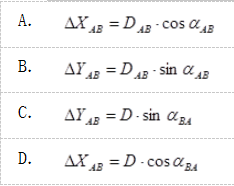
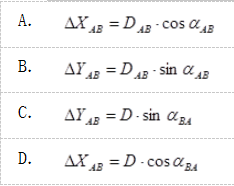
答案:A
解析:
首先,纵坐标的增量为x轴向的增量,可排除BC两项。其次,坐标正算方位角应该是从A到B,方位角为αAB,故为A项。
第5题:
下列命题中,正确的是( ).
A.单调函数的导函数必定为单调函数
B.设f´(x)为单调函数,则f(x)也为单调函数
C.设f(x)在(a,b)内只有一个驻点xo,则此xo必为f(x)的极值点
D.设f(x)在(a,b)内可导且只有一个极值点xo,f´(xo)=0
B.设f´(x)为单调函数,则f(x)也为单调函数
C.设f(x)在(a,b)内只有一个驻点xo,则此xo必为f(x)的极值点
D.设f(x)在(a,b)内可导且只有一个极值点xo,f´(xo)=0
答案:D
解析:
可导函数的极值点必定是函数的驻点,故选D.
第6题:
建立一个平面直角坐标系,描出点A(-2, 4),B(3, 4),画直线AB。若点C为直线AB上的任意一点,则点C的纵坐标是什么?想一想:
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标有什么特点?
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标有什么特点?
(1)如果一些点在平行与x轴的直线上,那么这些点的纵坐标相等
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标相等
第7题:
设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。
A.f(0)是f(x)在(-a,a)的极大值,但不是最大值
B.f(0)是f(x)在(-a,a)的最小值
C.f(0)是f(x)在(-a,a)的极大值,也是最大值
D.f(0)是曲线y=f(x)的拐点的纵坐标
B.f(0)是f(x)在(-a,a)的最小值
C.f(0)是f(x)在(-a,a)的极大值,也是最大值
D.f(0)是曲线y=f(x)的拐点的纵坐标
答案:C
解析:
第8题:
设X的概率密度与分布函数分别为f(x)和F(X),则下列选项正确是 ( )
A.P{X=x}=f(x)
B.P{X=x}=F(x)
C.P{X=x}<=F(x)
D.0
参考答案:C
第9题:
若已知αPA=158°48′16″,βA=91°02′10″,AP的水平距离为213.12m,则AP两点间的坐标方位角及纵坐标增量分别为( )。
A、249°50′26″和-73.45m
B、69°50′26″和73.45m
C、249°50′26″和-200.06m
D、69°50′26″和200.06m
B、69°50′26″和73.45m
C、249°50′26″和-200.06m
D、69°50′26″和200.06m
答案:B
解析:
AP两点间的坐标方位角αAP=158°48′16″+91°02′10″-180°=69°50′26″,纵坐标增量ΔY=213.12×cos69°50′26″=73.45m。
第10题:
已知某导线全长为S=720m,测得其纵坐标增量闭合差fx=+0.09m,横坐标增量闭合差fy=-0.47m,则导线的全长相对闭合差为( )。
A、1/2500
B、1/1900
C、1/1500
D、1/1300
B、1/1900
C、1/1500
D、1/1300
答案:C
解析:
由于导线边长观测值中有误差,故而角度观测值虽然经过导线角度闭合差的调整,但仍有剩余的误差。因此,由边长、方位角推算而得的坐标增量也有误差,从而产生纵坐标增量闭合差fx和横坐标增量闭合差fy。fx=∑Δx测-∑Δx理,fy=∑Δy测-∑Δy理,长度f为导线全长闭合差
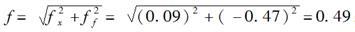
导线全长相对闭合差

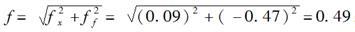
导线全长相对闭合差

