花样滑冰运动员通过自身竖直轴转动,开始时两臂张开,转动惯量为J0,角速度为W0;然后将手臂合拢使其转动惯量为2/3J0,则转动角速度变为()。A、2/3W0B、2/√3W0C、3/2W0D、√3/2W0
题目
花样滑冰运动员通过自身竖直轴转动,开始时两臂张开,转动惯量为J0,角速度为W0;然后将手臂合拢使其转动惯量为2/3J0,则转动角速度变为()。
- A、2/3W0
- B、2/√3W0
- C、3/2W0
- D、√3/2W0
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
有一半径为R的匀质水平圆转台,绕通过其中心且垂直圆台的轴转动,转动惯量为J,开始时有一质量为m的人站在转台中心,转台以匀角速度w0转动,随后人沿着半径向外跑去,当人到达转台边缘时,转台的角速度为()
A、w0
B、Jw0/mR^2
C、Jw0/(J+mR^2)
D、Jw0/(J+2mR^2)
参考答案:C
第2题:
一转动惯量为J的圆盘绕一固定轴转动,起初角速度为w。。设它所受阻力矩与转动角速度成正比,即M=-kw(k为正的常数),求圆盘的角速度从w。变为1/2w。时所需的时间。
答案:
解析:

第3题:
绕定轴转动的刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角速度的乘积。()
此题为判断题(对,错)。
参考答案:正确
第4题:
用转动惯量仪测定转动惯量实验中,所画的直线为以下哪两个量的关系()
- A、t―m
- B、t2―m
- C、t–1―m
- D、t–2―m
正确答案:D
第5题:
如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。

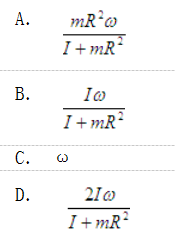

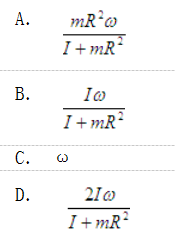
答案:B
解析:

第6题:
关于刚体的转动惯量,下列哪个是正确的?
A.转动惯量与转速有关
B.转动惯量与刚体的质量及分布有关
C.转动惯量与转轴的位置无关
D.转动惯量与转动的角速度有关
正确答案:B
第7题:
均质圆盘质量为m,半径为R,在铅垂面绕内O轴转动,图示瞬间角速度为ω,则其对O轴的动量矩大小为( )。


A.mRω
B.mRω/2
C.mR2ω/2
D.3mR2ω/2
B.mRω/2
C.mR2ω/2
D.3mR2ω/2
答案:D
解析:
根据质点的动量矩公式,体系对O点的动量矩为:
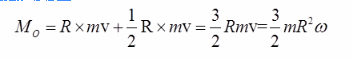
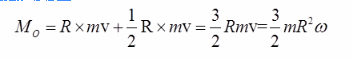
第8题:
花样滑冰者,开始自转时,手臂直身,其动能为E0=Jw0^2/2,然后将手臂收回,转动惯量减少到原来的1/3,此时的角速度变为w,动能变为E,则有关系()
A、w=3w0,E=E0
B、w=w0/3,E=3E0
C、w=w0/3,E=E0
D、w=3w0,E=3E0
参考答案:A
第9题:
设质量分布均匀的圆柱体的质量为m,半径为R,绕中心旋转时的角速度为ω,则此圆柱体的转动惯量为()。
- A、mR2
- B、0.5mR2
- C、mRω
正确答案:B
第10题:
飞轮转动时,转角为φ,则角速度(角频率)为()。
- A、φ/t
- B、dφ/dt
- C、d2φ/dt
正确答案:B
