初级统计师
若一组数据服从正态分布，则下列判断正确的有（）。A、正态随机变量落入其均值左右各1个标准差内的概率是68.27%B、正态随机变量落入其均值左右各2个标准差内的概率是68.27%C、正态随机变量落入其均值左右各2个标准差内的概率是95.45%D、正态随机变量落入其均值左右各3个标准差内的概率是99.73%E、正态随机变量落入其均值左右各4个标准差内的概率是99.73%
题目
若一组数据服从正态分布，则下列判断正确的有（）。
- A、正态随机变量落入其均值左右各1个标准差内的概率是68.27%
- B、正态随机变量落入其均值左右各2个标准差内的概率是68.27%
- C、正态随机变量落入其均值左右各2个标准差内的概率是95.45%
- D、正态随机变量落入其均值左右各3个标准差内的概率是99.73%
- E、正态随机变量落入其均值左右各4个标准差内的概率是99.73%
参考答案和解析
相似问题和答案
第1题：
以下是某产品直径的箱线图，则根据箱线图判定数据分布，最可能正确的是()。
A、数据服从正态分布
B、数据呈右偏态分布
C、数据呈左偏态分布
D、数据服从均匀分布
请帮忙给出正确答案和分析，谢谢!
答案：C
解析：对于标准正态分布的样本，只有极少值为异常值。异常值越多说明尾部越重，自由度越小（即自由变动的量的个数）；而偏态表示偏离程度，异常值集中在较小值一侧，则分布呈左偏态；异常值集中在较大值一侧，则分布呈右偏态。在上图中，异常值集中在较小值一侧，故为左偏分布。
第2题：
此题为判断题(对，错)。
第3题：
一组服从正态分布的数据，平均数为50．标准差为5，则Z值为一2.58的原始数据是
A．37.10 B．42.42 C．47.42 D．62．90
第4题：
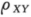=0,则X,Y一定相互独立；③X和Y都服从一维正态分布；④X,Y的任一线性组合服从一维正态分布.上述几种说法中正确的是().B.②③④
C.①③④
D.①②④
第5题：
设Xi (i=1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。
A．若Xi (i=1，2，…，n)服从正态分布，且分布参数相同，则
服从正态分布
B．若Xi (i=1，2，…，n)服从指数分布，且λ相同，则服从正态分布
C．若Xi(i=1，2，…，n)服从[a，b)上的均匀分布，则服从正态分布
D．无论Xi (i=1，2，…，n)服从何种分布，其均值都服从正态分布
解析：若总体服从正态分布，无论样本量大小，其样本均值X都服从正态分布。
第6题：
若质量数据服从正态分布，则质量特性值落入区间()的概率为99.73%。
A、3σ
B、μ+3σ
C、-3σ
D、μ±3σ
第7题：
设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。
A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布
B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布
C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布
D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布
解析：中心极限定理指出，无论共同的分布是什么，只要随机变量的个数n相当大时，的分布总近似于正态分布。
第8题：
A.69.8
B.47.4
C.50.2
D.37.2
第9题：
B.(X,Y)一定服从二维正态分布
C.X与Y不相关,则X,Y相互独立
D.若X与Y相互独立,则X-Y服从正态分布
第10题：
B.47.4
C.50.2
D.37.2
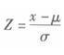
的逆运算，将已知数据代入公式可得此时的原始分数x为50. 2。