设f(x)在(-∞,+∞)二阶可导,f′(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值()?A、x=x0是f(x)的唯一驻点B、x=x0是f(x)的极大值点C、f″(x)在(-∞,+∞)恒为负值D、f″(x0)≠0
题目
设f(x)在(-∞,+∞)二阶可导,f′(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值()?
- A、x=x0是f(x)的唯一驻点
- B、x=x0是f(x)的极大值点
- C、f″(x)在(-∞,+∞)恒为负值
- D、f″(x0)≠0
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
曲线y=f(x)在点(x0,f(x0))有拐点,且f''(x0)存在,则f''(x0)=1。()
此题为判断题(对,错)。
参考答案:错
第2题:
下列命题正确的是()
A.函数f(x)的导数不存在的点,一定不是f(x)的极值点
B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
D.若函数f(x)在点x0处连续,则f'(x0)一定存在
B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
D.若函数f(x)在点x0处连续,则f'(x0)一定存在
答案:C
解析:
根据函数在点x0处取极值的必要条件的定理,可知选项C是正确的.
第3题:
以下结论正确的是()。
A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.
B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.
C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.
D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
参考答案:C
第4题:
函数y=f(x) 在点x=x0处取得极小值,则必有:
A. f'(x0)=0
B.f''(x0)>0
C. f'(x0)=0且f''(x0)>0
D.f'(x0)=0或导数不存在
B.f''(x0)>0
C. f'(x0)=0且f''(x0)>0
D.f'(x0)=0或导数不存在
答案:D
解析:
提示 已知y=f(x)在x=x0处取得极小值,但在题中f(x)是否具有一阶、二阶导数,均未说明,从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况,如y= x 在x=0处导数不存在,但函数y= x 在x=0取得极小值。
第5题:
设f(x)在(-∞,+∞)二阶可导,f'(x0)=0。问f(x)还要满足以下哪个条件,则f(x0)必是f(x)的最大值?
A.x=x0是f(x)的唯一驻点
B.x=x0是f(x)的极大值点
C.f"(x)在(-∞,+∞)恒为负值
D.f"(x0)≠0
B.x=x0是f(x)的极大值点
C.f"(x)在(-∞,+∞)恒为负值
D.f"(x0)≠0
答案:C
解析:
提示:f"(x)在(-∞,+∞)恒为负值,得出函数f(x)图形在(-∞,+∞)是向上凸,又知f'(x0)=0。故当x0时,f'(x)0)取得极大值。且f"(x)0)是f(x)的最大值。
第6题:
函数f(x)二阶可导,且f’(x0)=0,则点(x0,f(x0))为曲线y=f(x)的拐点。()
此题为判断题(对,错)。
参考答案:错误
第7题:
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
答案:
解析: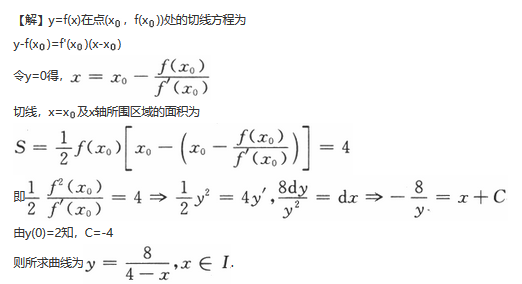
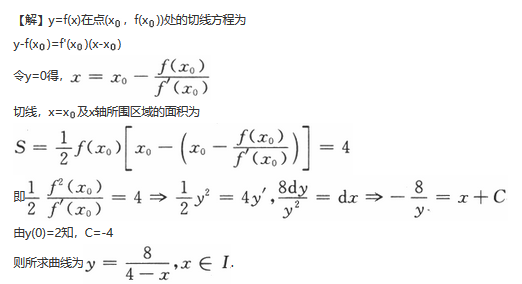
第8题:
设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。
A、0
B、π/2
C、锐角
D、钝角
参考答案:C
第9题:
函数y=f(x)在点x=x0处取得极小值,则必有:
A.f′(x0)=0
B.f′′(x0)>0
C. f′(x0)=0 且 f(xo)>0
D.f′(x0)=0 或导数不存在
B.f′′(x0)>0
C. f′(x0)=0 且 f(xo)>0
D.f′(x0)=0 或导数不存在
答案:D
解析:
已知y=f(x)在x=x0处取得极小值,但在题中f(x)是否具有一阶、二阶导数,均未说明,从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况,如 :y= x 在x=0处导数不存在,但函数y= x 在x=0取得极小值。
第10题:
设f(x)在(-∞,+∞)上是偶函数,若f'(-x0)=-K≠0,则f(x0)等于:


答案:B
解析:
提示:利用结论“偶函数的导函数为奇函数”计算。
f(-x)=f(x),求导-f'(-x)=f'(x),即f'(-x)=-f'(x)。将x=x0代入,得f'(-x0)=-f'(x0),解出f'(x0)=K。
f(-x)=f(x),求导-f'(-x)=f'(x),即f'(-x)=-f'(x)。将x=x0代入,得f'(-x0)=-f'(x0),解出f'(x0)=K。
