注册电气工程师
设随机变量X服从正态分布N（1，4）.已知φ（1）=a，则P（-1）=（）A、a-1B、2a+1C、a+1D、2a-1
题目
设随机变量X服从正态分布N（1，4）.已知φ（1）=a，则P（-1）=（）
- A、a-1
- B、2a+1
- C、a+1
- D、2a-1
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设随机变量X服从正态分布N(0，1)，P(x>1)=0．2，则P(-1
A.0．1
B.0．3
C.0.6
D.0．8
B.0．3
C.0.6
D.0．8
答案：C
解析：
P(-11)=0．6。
第2题：
设服从N(0,1)分布的随机变量X，其分布函数为φ(x)，如果φ(1)=0.84，则P|x|≤1的值是( )。
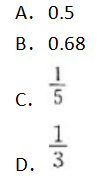
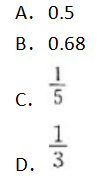
答案：B
解析：
X～N(0,1)，P{|x|≤1)=2Φ(1)-1=0.68
第3题：
设随机变量X服从对数正态分布,E(1nX)=5,Var(1nX)=4,则P(X<460)=________,已知1n460=6.1312。
A．0.6380
B．0.7140
C．0.7863
D．0.8032
正确答案：B
第4题：
设随机变量X服从正态分布N(-1，9)，则随机变量Y=2-X服从( ).
A.正态分布N(3，9)
B.均匀分布
C.正态分布N(1，9)
D.指数分布
B.均匀分布
C.正态分布N(1，9)
D.指数分布
答案：A
解析：
第5题：
设随机变量X服从正态分布N(1，4).已知Φ(1)=a，则P(-1＜X≤3)等于
A.a-1
B.2a+1
C.a+1
D.2a-1
B.2a+1
C.a+1
D.2a-1
答案：D
解析：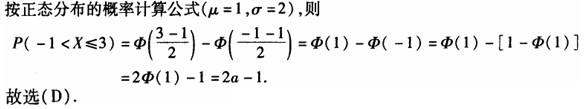
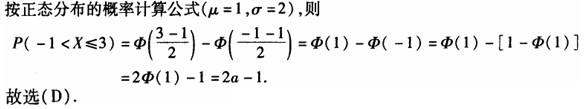
第6题：
设二维随机变量(X，Y)服从正态分布N(1，0;1，1;0)，则P{XY-Y<0}=_________.
答案：
解析：
(X，Y)～N(1，0;1，1;0)，所以X与Y相互独立，且X～N(1，1)，Y～N(0，1)也就有(X-1)～N(0，1)与Y相互独立，再根据对称性：P{X-1<0}=P{X-1>0}=P(Y<0)=P{Y>0}=
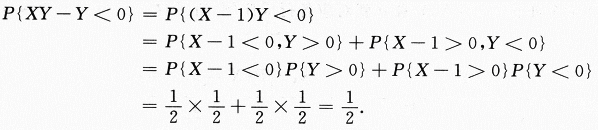
.不难求出P{XY-Y<0}的值.
.不难求出P{XY-Y<0}的值.
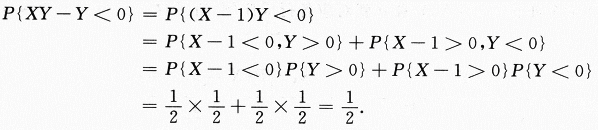
第7题：
设随机变量X服从正态分布N(μ，1).已知P(X≤μ-3)=c，则P(μ＜x＜μ+3)等于( ).
A.2c-1
B.1-c
C.0.5-c
D.0.5+c
B.1-c
C.0.5-c
D.0.5+c
答案：C
解析：
由于P(X≤μ-3)=Φ((μ-3)-μ)=Φ(-3)=c，因此，P(μ＜X＜μ+3)=Φ((μ+3)-μ)-Φ(μ-μ)=Φ(3)-Φ(0)=[1-Φ(-3)]-0.5=(1-c)-0.5=0.5-c.故选C.
第8题：
设随机变量X~N(1,4),则P()
A.1-2Φ(0.5)
B.2Φ(0.5)-1
C.Φ(0.5)-1
D.1-Φ(0.5)
参考答案：B
第9题：
设随机变量X服从正态分布N(0，1)，对给定的α(0<α<1)数μ满足P{X>μα}=α，若P{|X|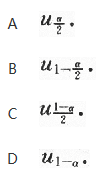
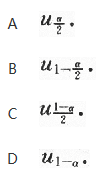
答案：C
解析：
第10题：
设两个相互独立的随机变量X和Y分别服从正态分布N(0，1)和N(1，1)，则
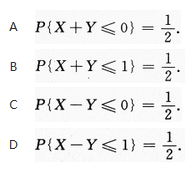
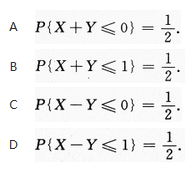
答案：B
解析：
【简解】首先应看到，X+Y和X-Y均为一维正态分布的随机变量.其次要看到，如果z～N(μ，σ^2)，则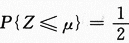
，反之，如果
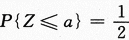，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.
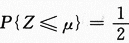，反之，如果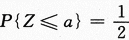，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.