注册电气工程师
微分方程y"=y’2的通解是（）（C1、C2为任意常数）。A、lnx+CB、ln（x+C）C、C2+lnD、C2-ln
题目
微分方程y"=y’2的通解是（）（C1、C2为任意常数）。
- A、lnx+C
- B、ln（x+C）
- C、C2+ln
- D、C2-ln
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
微分y″=x+sinx方程的通解是( )。(c1，c2为任意常数)
A.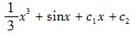
B.
C.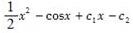
D.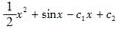
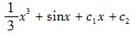
B.
C.
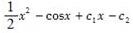
D.
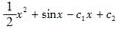
答案：B
解析：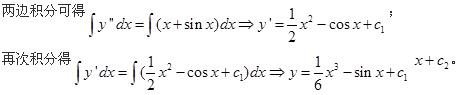
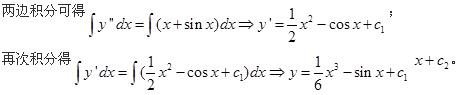
第2题：
微分方程(1+y)dx-(1-x)dy=0的通解是(c为任意常数)：
答案：C
解析：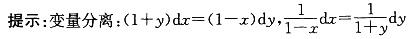
积分得：ln(1-x)+ln(1+y)=lnc。
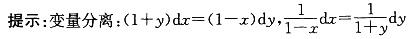积分得：ln(1-x)+ln(1+y)=lnc。第3题：
在下列微分方程中，以函数y＝C1e^－x＋C2e^4x（C1，C2为任意常数）为通解的微分方程是（ ）。
A． y″＋3y′－4y＝0
B． y″－3y′－4y＝0
C． y″＋3y′＋4y＝0
D． y″＋y′－4y＝0
B． y″－3y′－4y＝0
C． y″＋3y′＋4y＝0
D． y″＋y′－4y＝0
答案：B
解析：
由题意知，二阶常系数齐次线性微分方程的特征方程的两个根为－1和4，只有B项满足。
【总结】求二阶常系数齐次线性微分方程y″＋py′＋qy＝0的通解的步骤：
①写出微分方程的特征方程r2＋pr＋q＝0；
②求出特征方程的两个根r1，r2；
③根据r1，r2的不同情形，写出微分方程的通解：
a．当r1≠r2，
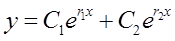
b．当r1＝r2，
c．一对共轭复根r1，2＝α±βi，y＝eαx（C1cosβx＋C2sinβx）。
由题意知，二阶常系数齐次线性微分方程的特征方程的两个根为－1和4，只有B项满足。
【总结】求二阶常系数齐次线性微分方程y″＋py′＋qy＝0的通解的步骤：
①写出微分方程的特征方程r2＋pr＋q＝0；
②求出特征方程的两个根r1，r2；
③根据r1，r2的不同情形，写出微分方程的通解：
a．当r1≠r2，
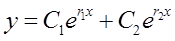
b．当r1＝r2，
c．一对共轭复根r1，2＝α±βi，y＝eαx（C1cosβx＋C2sinβx）。
第4题：
微分方程y′′-4y=4的通解是(C1，C2为任意常数）：
A.C1e2x-C2e-2x+1
B. C1e2x+C2e-2x-1
C.e2x-e-2x+1
D. C1e2x+C2e-2x-2
B. C1e2x+C2e-2x-1
C.e2x-e-2x+1
D. C1e2x+C2e-2x-2
答案：B
解析：
第5题：
微分方程y′′=x+sinx的通解是(C1，C2为任意常数）：
答案：B
解析：
第6题：
若A、B为非零常数，C1、C2为任意常数，则微分方程y″+k2y=cosx的通解应具有形式( )。
A.C1coskx+C2sinkx+Asinx+Bcosx
B.C1coskx+C2sinkx+Axcosx
C.C1coskx+C2sinkx+Axsinx
D.C1coskx+C2sinkx+Axsinx+Bxcosx
B.C1coskx+C2sinkx+Axcosx
C.C1coskx+C2sinkx+Axsinx
D.C1coskx+C2sinkx+Axsinx+Bxcosx
答案：C
解析：
第7题：
函数y=c1e2x+c2(其中c1、c2是任意常数)是微分方程
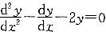
的( )。
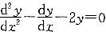
的( )。
A.通解
B.特解
C.不是解
D.是解，但不是通解也不是特解
B.特解
C.不是解
D.是解，但不是通解也不是特解
答案：D
解析：
y=c1e2x+c2=c3e2x经验证是方程的解，但不是通解也不是特解
第8题：
微分方程y″-4y=4的通解是( )。(c1，c2为任意常数)
A.
B.
C.e2x-e-2x+1
D.c1e2x+c2e-2x-2
B.
C.e2x-e-2x+1
D.c1e2x+c2e-2x-2
答案：B
解析：
第9题：
微分方程y''+2y=0的通解是：
(A,B为任意常数）
(A,B为任意常数）
答案：D
解析：
提示:本题为二次常系数线性齐次方程求通解，写出方程对应的特征方程r2+2 = 0,r =
第10题：
微分方程y''=(y')2的通解是：
A. lnx+c B. ln(x+c)
C. c2+ln x+c1 D. c2-lnlx+c1
(以上各式中，c1、c2为任意常数）
A. lnx+c B. ln(x+c)
C. c2+ln x+c1 D. c2-lnlx+c1
(以上各式中，c1、c2为任意常数）
答案：D
解析：
提示:此题为可降阶的高阶微分方程，按方程不显含变量y计算。
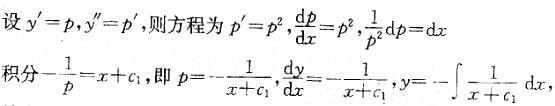
y=c2-lnlx+c1
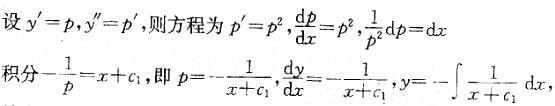
y=c2-lnlx+c1