计算机图形学

在齐次坐标系中，若用矩阵来表示各种运算，则比例和旋转变换是矩阵乘法运算，而平移变换是矩阵加法运算。

题目

在齐次坐标系中，若用矩阵来表示各种运算，则比例和旋转变换是矩阵乘法运算，而平移变换是矩阵加法运算。

如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案

第1题：

平面图形以基点P(3,2)旋转θ角,求其图形变换矩阵T,所需的变换有()。

A.比例变换

B.平移变换

C.错切变换

D.旋转变换


正确答案：BD

第2题：

为什么矩阵的并行加法运算必须将运算双方的相应分量置于局部存储器的同一单元?


答案：由于矩阵相加的特点是各个矩阵各个对应分量之间相加，不对应分量之间不做任何操作。也就是说，同一个矩阵分量可执行相同的操作。而将对应分量置于同一局部存储器的同一单元，则在执行加法操作时可以省去寻址操作，这样可以提高并行算法的效率。

第3题：

在利用矩阵进行图形三维变换时,我们只用3×3矩阵无法完成的变换操作是()

A.平移

B.旋转

C.错切

D.以上说法都不对


正确答案:A

第4题：

阅读下列说明和C代码，回答问题1至问题3

【说明】 某工程计算中要完成多个矩阵相乘（链乘）的计算任务。 两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数，计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法，计算Am×n*Bn×p，需要m*n*p次乘法运算。 矩阵相乘满足结合律，多个矩阵相乘，不同的计算顺序会产生不同的计算量。以矩阵A110×100，A2100×5，A35×50三个矩阵相乘为例，若按（A1*A2）*A3计算，则需要进行10*100*5+10*5*50=7500次乘法运算；若按A1*（A2*A3）计算，则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。 矩阵链乘问题可描述为：给定n个矩阵


答案：
解析：

第5题：

以下关于图形变换的论述那些是错误的()。

A、错切变换虽然可引起图形角度的改变，但不会发生图形畸变

B、平移变换不改变图形大小和形状，只改变图形位置

C、任意一个变换序列均可表示为一个组合变换矩阵，该组合变换矩阵是基本变换矩阵的和

D、旋转变换后各图形部分间的线性关系和角度关系不变，变换后直线的长度不变


参考答案：C

第6题：

证明二维旋转和比例变换的组合变换时，变换矩阵可交换相乘


参考答案：

第7题：

阐述矩阵乘法的运算过程。并用矩阵乘积形式表示如下线性方程组。

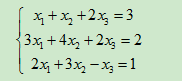
用初等变换的方法求解上述线性方程组。


答案：

第8题：

矩阵与标量的加法是指标量本身与矩阵元素进行加法运算。()


正确答案：√

第9题：

AES算法中对于每个明文分组的加密过程按照如下顺序进行()。

A.将明文分组放入状态矩阵中、AddRoundKey变换、10轮循环运算

B.AddRoundKey变换、将明文分组放入状态矩阵中、10轮循环运算

C.10轮循环运算、AddRoundKey变换、将明文分组放入状态矩阵中

D.AddRoundKey变换、10轮循环运算、将明文分组放入状态矩阵中


参考答案：A

第10题：

二维图形变换使用了齐次坐标表示法，其变换矩阵是（）。

  • A、2×2矩阵 
  • B、3×3矩阵 
  • C、4×4矩阵 
  • D、5×5矩阵

正确答案:B

更多相关问题
相关内容