问答题编一个程序,把一张1元的钞票换成5分,2分和1分的硬币,要求每种至少一枚,并且所换硬币数不超过30枚。请问,有哪几种换法?
题目
参考答案和解析
Console.WriteLine("一分:/t二分:/t五分:");
for(i=1;i<=100;i++)
for(j=1;j<=50;j++)
for(k=1;k<=20;k++)
if(i+2*j+5*k==100&&i+j+k<=30)Console.WriteLine("{0}枚/t{1}枚/t{2}枚",i,j,k);
相似问题和答案
第1题:
A.硬币模块未安装到位
B.未输入补币数
C.纸币钱箱满
D.硬币储币箱空
第2题:
小李的储蓄罐有100枚硬币,他把其中的贰分币全部换成等值的伍分币,硬币总数变为73枚,他又把壹分币换成等值的伍分币,硬币i总数变为33枚,他原来共有多少钱???
2分换成5分,总数减少了100-73=27个
5个2分 换成 2个5分 减少3个
45 18 27
按照比例,原来2分硬币是45个,换成了18个5分硬币
73个变成了33个,
减少了40个
5个 换成 1个 减少了4个
50 10 40
同样的比例的方法可得1分硬币是50个
总结下100个硬币中,2分45个,1分50个,那剩下的5个是5分的。
总钱数算一下就是90+50+25=165分
第3题:
将一枚硬币投掷两次,至少出现一次正面的概率为( )。
A.0.25
B.0.50
C.0.75
D.1.00
第4题:
设有9 个硬币,其中有 1 分、5分、1角以及 5角四种,且每种硬币至少有 1个。若这 9个硬币总值是 1.77元,则5分硬币必须有几个?( )
A.1
B.2
C.3
D.4
每种硬币至少有1个,则知四种硬币各1个共0.66元,总值为1.77元,则需增加1.11元,从而需硬币1分1个,硬币5角2个,最后还需1角,从1角硬币1个或2个5分硬币中选择,题意要9个硬币,宜选择2个5分硬币,因而有3个5分硬币。故答案为C。
第5题:
一枚硬币投掷三次,或三枚硬币各掷一次,出现两次或两次以上正面的概率是1/2。()
第6题:
:通常认为,抛掷一枚质量均匀的硬币的结果是随机的。但实际上,抛掷结果是由抛掷硬币的冲力和初始高度共同决定的。尽管如此,对抛掷硬币的结果作出准确预测还是十分困难。下面哪一项最有助于解释题干所说到的现象,即抛掷结果被某些因素决定,但预测却很困难( )
A.很长时间以来,抛掷硬币已被用作随机事件的典型例证
B.如果抛掷一枚质量不均匀的硬币。其结果总能够被精确地预测
C.如果抛掷硬币的初始高度保持稳定不变。则抛掷硬币的结果将仅由抛掷冲力决定
D.对抛掷硬币结果的准确预测,要求极其精确地估计抛掷硬币的初始高度和冲力
已知现象Q由P1和P2两个因素决定,但现象Q仍难以预测。原因何在?当然P1和P2两个因素难以确定。即D项正确。
第7题:
硬币整点有( )和工具整点硬币两种方法。
手工整点硬币
第8题:
一枚均匀的硬币连续抛掷3次,求3次均为上面的概率。
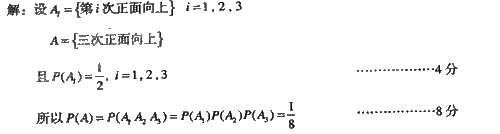
第9题:
设有9个硬币,其中有1分、5分、3角以及5角四种,且每种硬币至少有1个。若这9个硬币总值是1.77元,则5分硬币必须有几个?()
A.1 B.2 C.3 D.4
每种硬币至少有1个,则知四种硬币各1个共0.66元,总值为1.77元,则需增加1.11元,从而需硬币1分1个,硬币5角2个,最后还需1角,从l角硬币1个或2个5分硬币中选择,题意要9个硬币,宜选择2个5分硬币,因而有3个5分硬币。故答案为C。
第10题:
小李的储蓄罐有100枚硬币,他把其中的贰分币全部换成等值的伍分币,硬币总数变为73枚,他又把壹分币换成等值的伍分币,硬币i总数变为33枚,他原来共有多少钱???
题目没有说清楚原来储蓄罐里的硬币一共有哪几种类型 我们假设硬币一共有三种类型,1分,2分,5分 最简单的算法: 1分,2分的硬币全部换成了等值的5分硬币,(注意是全部,所以可以用简便算法,不用算换的个数) 100枚硬币变成了33枚5分的硬币 所以原来共有33*5分=1元6角5分
