精算模型
单选题一个随机抽取的样本包括100个数据，用指数分布拟合时，以极大似然估计去求分布的参数，此时极大化的似然函数值为-159.4。继续用伽玛分布拟合这组数据，如果根据似然比检验，伽玛分布的拟合效果在5%显著性水平下优于指数分布的话，则用极大似然估计求伽玛分布模型的参数时，最大化的似然函数值至少为（ ）。A -156.45B -137..46C -154.37D -147.96E -157.48
题目
单选题
一个随机抽取的样本包括100个数据，用指数分布拟合时，以极大似然估计去求分布的参数，此时极大化的似然函数值为-159.4。继续用伽玛分布拟合这组数据，如果根据似然比检验，伽玛分布的拟合效果在5%显著性水平下优于指数分布的话，则用极大似然估计求伽玛分布模型的参数时，最大化的似然函数值至少为（ ）。
A
-156.45
B
-137..46
C
-154.37
D
-147.96
E
-157.48
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设总体X的分布函数为
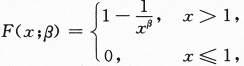
其中未知参数β>1，X1，X2，…，Xn为来自总体X的简单随机样本，求：
(Ⅰ)β的矩估计量；(Ⅱ)β的最大似然估计量.
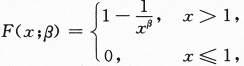
其中未知参数β>1，X1，X2，…，Xn为来自总体X的简单随机样本，求：
(Ⅰ)β的矩估计量；(Ⅱ)β的最大似然估计量.
答案：
解析：
第2题：
设总体X的密度函数为f(x)=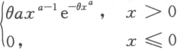
,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
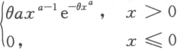,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.答案：
解析：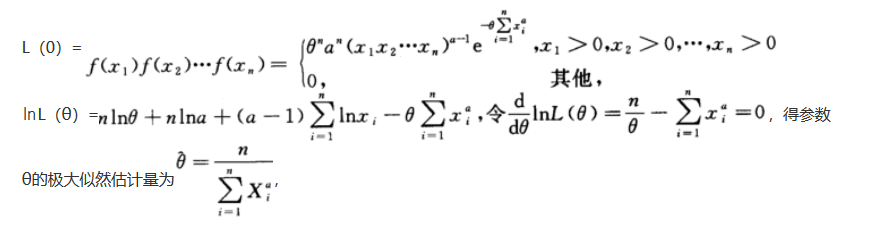
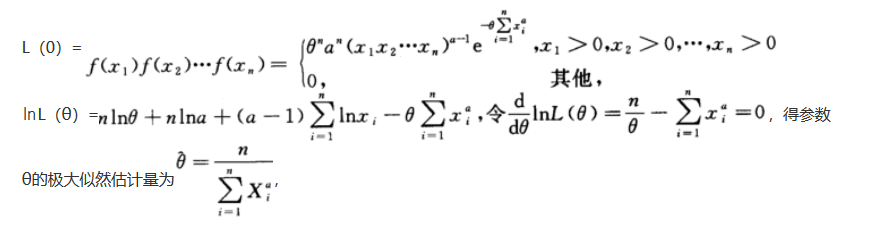
第3题：
已知总体X服从参数为λ的指数分布,设X1,X2,…,Xn是子样观察值,求λ的极大似然估计。
参考答案：
第4题：
设总体X的概率分布为
其中θ(0<0<
)是未知参数，利用总体X的如下样本值3,1,3,0,3,1,2,3，求θ的矩估计值和最大似然估计值，
其中θ(0<0<
)是未知参数，利用总体X的如下样本值3,1,3,0,3,1,2,3，求θ的矩估计值和最大似然估计值，答案：
解析：
第5题：
设总体X～F（x,θ）=
,样本值为1,1,3,2,l,2,3,3,求θ的矩估计和最大似然估计.
,样本值为1,1,3,2,l,2,3,3,求θ的矩估计和最大似然估计.答案：
解析：
(1)X为离散型随机变量，其分布律为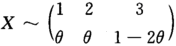
，E(X)=3-3θ.
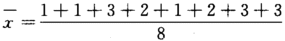=2，令3-3θ=2得θ的矩估计值为
.
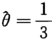(2)L(1,1,3,2,1,2,3,3;θ)=P(X=l)P(X=1)…P(X=3)=θ^3×θ^2×（1-。得θ的最大似然估计值为2θ)^3,InL（θ）-51nθ+31n(l-2θ)，令
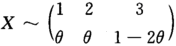，E(X)=3-3θ.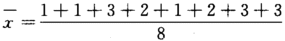=2，令3-3θ=2得θ的矩估计值为.
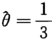(2)L(1,1,3,2,1,2,3,3;θ)=P(X=l)P(X=1)…P(X=3)=θ^3×θ^2×（1-。得θ的最大似然估计值为2θ)^3,InL（θ）-51nθ+31n(l-2θ)，令
第6题：
设总体X的分布律为P（X=k)
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.答案：
解析：
第7题：
设总体X的密度函数为f(x)=
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.答案：
解析：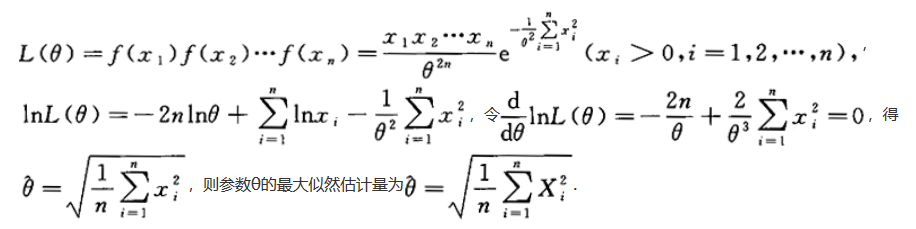
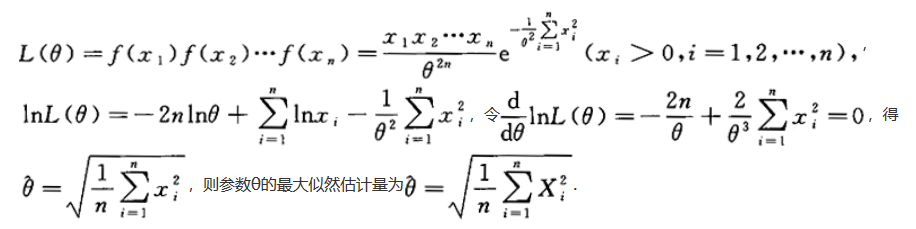
第8题：
逻辑回归优化的目标函数为()。
A.贝叶斯定理
B.特征独立假设
C.极大似然估计
D.对数似然函数
正确答案:D
第9题：
设总体X～U［0,θ］,其中θ>0,求θ的极大似然估计量,判断其是否是θ的无偏估计量.
答案：
解析：
第10题：
设总体X的概率分布为
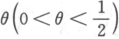
是未知参数,用样本值3,1,3,0,3,1,2,3求θ的矩估计值和最大似然估计值,
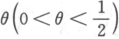
是未知参数,用样本值3,1,3,0,3,1,2,3求θ的矩估计值和最大似然估计值,
答案：
解析：