某产品X的市场需求函数D?供给函数S分别为:D=10-2Px+0.5I+4PyS=10+2t+3.5PxPx为X产品的价格,Py为相关产品Y的价格,I为消费者收入,t代表生产技术水平?(1)求当I=22,Py=5.5,t=2.75时的均衡价格和均衡数量?(2)在(1)的情形下,如果Py下降至2.75,其均衡价格和均衡数量将如何变化?(3)在(1)的情形下,如果t上升至5.5,均衡价格和均衡数量将如何变化?
题目
某产品X的市场需求函数D?供给函数S分别为:
D=10-2Px+0.5I+4Py
S=10+2t+3.5Px
Px为X产品的价格,Py为相关产品Y的价格,I为消费者收入,t代表生产技术水平?
(1)求当I=22,Py=5.5,t=2.75时的均衡价格和均衡数量?
(2)在(1)的情形下,如果Py下降至2.75,其均衡价格和均衡数量将如何变化?
(3)在(1)的情形下,如果t上升至5.5,均衡价格和均衡数量将如何变化?
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
假定某商品市场的需求函数为Qd=12-P,供给函数为Qs=-2+P,则()。
A.均衡数量为5
B.均衡价格为6
C.均衡价格为7
D.均衡数量为4
答案:A、C
解析:需求函数为Qd=12-P,供给函数为Qs=-2+P
供求均衡时:12-P=-2+P,求得:Q=5,P=7
第2题:
已知某完全竞争的成本递增行业的长期供给函数LS= 5500 +300P。试求: (1)当市场需求函数为D=8000 - 200P时,市场的长期均衡价格和均衡产量。 (2)当市场需求增加时,市场需求函数为D=10000 - 200P时,市场长期均衡价格和均衡产量。 (3)比较(1)和(2),说明市场需求变动对成本递增行业的长期均衡价格和均衡产量的影响。
答案:
解析:
(1)根据在完全竞争市场长期均衡时的条件LS =D,即有5500 +300P= 8000 - 200P,解得Pe =5。 把Pe=5代入LS函数,得Q。=5500 +300×5=7000。 所以,市场的长期均衡价格和均衡数量分别为Pe=5、Qe=7000。 (2)同理,根据LS =D,有5500+ 300P =10000 - 200P,解得Pe=9。 以Pe=9代人LS函数,得Qe=5500 +300×9=8200。 所以,市场的长期均衡价格和均衡数量分别为Pe=9、Qe=8200。 (3)比较(1)和(2)可得,对于完全竞争的成本递增行业而言,市场需求增加,会使市场的均衡价格上升,即由Pe=5上升为Pe=9,市场的均衡数量也增加,即由Qe=7000增加为Qe=8200。也就是说,市场需求与均衡价格成同方向的变动,与均衡数量也成同方向的变动。
第3题:
对一般的商品来说,当其供给不变时,如果其需求增加,则该商品的( )。
A.均衡价格上升和均衡数量减少
B.均衡价格上升和均衡数量增加
C.均衡价格下降和均衡数量减少
D.均衡价格下降和均衡数量增加
正确答案:B
理解供给或需求的变动对均衡价格和均衡数量的影响。
理解供给或需求的变动对均衡价格和均衡数量的影响。
第4题:
在需求不变的情况下,供给的变动将引起( )。
A.均衡价格同方向变动
B.均衡价格反方向变动
C.均衡数量同方向变动
D.均衡数量反方向变动
E.均衡价格和均衡数量不变动
B.均衡价格反方向变动
C.均衡数量同方向变动
D.均衡数量反方向变动
E.均衡价格和均衡数量不变动
答案:B,C
解析:
在需求不变的情况下,供给增加会使供给曲线向右平移,从而使得均衡价格下降,均衡数量增加;供给减少会使供给曲线向左平移,从而使得均衡价格上升,均衡数量减少。因此,供给的变动引起均衡价格反方向变动,均衡数量同方向变动。
第5题:
已知某一时期内某商品的需求函数为Q’=50-5P,供给函数为Q=-10+5P (1)求均衡价格Pe和均衡数量Qe,并作出几何图形。 (2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd= 60 -5P。求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。 (3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs= -5 +5P。求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。 (4)利用(1)、(2)和(3).说明静态分析和比较静态分析的联系和区别。 (5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格与均衡数量的影响。
答案:
解析:
(1)已知在均衡价格水平上供给等于需求,将需求函数Qd= 50一5P和供给函数Qs= - 10 +5P代入Qd=Qs,有50 -5P= - 10 +5P,得Pe=6。 把Pe=6代入需求函数Qd =50 -5P,得Qe=50 -5 x6 =20,所以均衡价格和均衡数量分别为Pe=6、Qe=20,如图2-5所示。

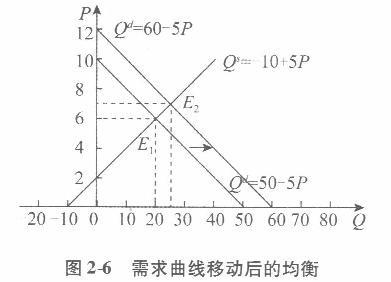
(2)消费者收入变化,则需求变化,从而需求曲线向右移动,形成新的均衡。将由于消费者收入水平提高而产生的需求函数Qd=60 -5P和原供给函数Qs= -10 +5P,代入均衡条件Qd= Qs,有60 -5P= - 10 +5P,得Pe =7。 把Pe =7代入Qd =60 -5P,得Q。=60 -5 x7 =25,或者将均衡价格Pe=7代入Qe=- 10 +5P,得Qe= -10 +5 x7= 25。所以,均衡价格和均衡数量分别为Pe=7、Qe=25,如图2-6所示。
(3)生产技术水平变动,从而供给曲线向右移动,形成新的均衡将原需求函数Qd =50 -5P和由于技术水平提高而产生的供给函数Qs= -5 +5P,代入均衡条件Qd=Qs,有50 - SP=-5 +5P,得Pe= 5.5。 把Pe=5.5代人Qd =50 -5P,得Qe=50 -5 x5.5 =22.5。或者以均衡价格Pe=5.5代入Qs=-5 +5P,得Qe=-5 +5 x5.5 =22.5。所以,均衡价格和均衡数量分别为Pe=5.5、Qe= 22.5,如图2-7所示。
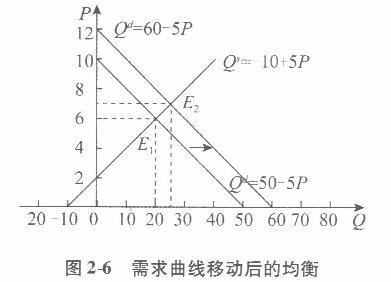
(4)静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。以(1)为例,在图2-5中,均衡点E就是一个体现了静态分析特征的点。它是在给定的供求力量的相互作用下所达到的一个均衡点。在此,给定的供求力量分别用给定的供给函数Qs=- 10 +5P和需求函数Qd =50 -5P表示,均衡点E具有的特征是:均衡价格Pe=6且当Pe=6时,有Qd= Qs =Qe=20;同时,均衡数量Qe=20且当Qe=20时,有Pd=Ps=Pe=6。 依此类推,以上所描述的关于静态分析的基本要点,在(2)及图2-6和(3)及图2-7中的每一个单独的均衡点Ei(i=1,2)都得到了体现。 比较静态分析是考察当原有的条件发生变化时,原有的均衡状态会发生什么变化,并分析比较新旧均衡状态。以(2)为例加以说明。在图2-6中,由均衡点E1变动到均衡点E2,就是一种比较静态分析。它表示当需求增加即需求函数发生变化时对均衡点的影响。比较新、旧两个均衡点E和E2可以很清楚地看到:由于需求增加导致需求曲线右移,最后使得均衡价格由6上升为7,同时,均衡数量由20增加为25。也可以这样理解比较静态分析:在供给函数保持不变的前提下,由于需求函数中的外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量的数值发生变化,其结果为均衡价格由原来的6上升为7,同时,均衡数量由原来的20增加为25。类似地,利用(3)及其图2-7也可以说明比较静态分析方法的基本要点。 (5)比较(1)和(2)可得,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了。 比较(1)和(3)可得,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了。 一般地,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量成同方向变动。

(2)消费者收入变化,则需求变化,从而需求曲线向右移动,形成新的均衡。将由于消费者收入水平提高而产生的需求函数Qd=60 -5P和原供给函数Qs= -10 +5P,代入均衡条件Qd= Qs,有60 -5P= - 10 +5P,得Pe =7。 把Pe =7代入Qd =60 -5P,得Q。=60 -5 x7 =25,或者将均衡价格Pe=7代入Qe=- 10 +5P,得Qe= -10 +5 x7= 25。所以,均衡价格和均衡数量分别为Pe=7、Qe=25,如图2-6所示。

(3)生产技术水平变动,从而供给曲线向右移动,形成新的均衡将原需求函数Qd =50 -5P和由于技术水平提高而产生的供给函数Qs= -5 +5P,代入均衡条件Qd=Qs,有50 - SP=-5 +5P,得Pe= 5.5。 把Pe=5.5代人Qd =50 -5P,得Qe=50 -5 x5.5 =22.5。或者以均衡价格Pe=5.5代入Qs=-5 +5P,得Qe=-5 +5 x5.5 =22.5。所以,均衡价格和均衡数量分别为Pe=5.5、Qe= 22.5,如图2-7所示。

(4)静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。以(1)为例,在图2-5中,均衡点E就是一个体现了静态分析特征的点。它是在给定的供求力量的相互作用下所达到的一个均衡点。在此,给定的供求力量分别用给定的供给函数Qs=- 10 +5P和需求函数Qd =50 -5P表示,均衡点E具有的特征是:均衡价格Pe=6且当Pe=6时,有Qd= Qs =Qe=20;同时,均衡数量Qe=20且当Qe=20时,有Pd=Ps=Pe=6。 依此类推,以上所描述的关于静态分析的基本要点,在(2)及图2-6和(3)及图2-7中的每一个单独的均衡点Ei(i=1,2)都得到了体现。 比较静态分析是考察当原有的条件发生变化时,原有的均衡状态会发生什么变化,并分析比较新旧均衡状态。以(2)为例加以说明。在图2-6中,由均衡点E1变动到均衡点E2,就是一种比较静态分析。它表示当需求增加即需求函数发生变化时对均衡点的影响。比较新、旧两个均衡点E和E2可以很清楚地看到:由于需求增加导致需求曲线右移,最后使得均衡价格由6上升为7,同时,均衡数量由20增加为25。也可以这样理解比较静态分析:在供给函数保持不变的前提下,由于需求函数中的外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量的数值发生变化,其结果为均衡价格由原来的6上升为7,同时,均衡数量由原来的20增加为25。类似地,利用(3)及其图2-7也可以说明比较静态分析方法的基本要点。 (5)比较(1)和(2)可得,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了。 比较(1)和(3)可得,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了。 一般地,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量成同方向变动。
第6题:
封闭经济总需求与总供给模型: c=1oo+o. 8Y I=1000 - 2r名义货币供给量Ms =800实际货币需求量
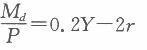
政府购买支出G=500短期总生产函数Y=20L劳动供给
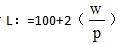
劳动需求
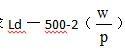
W为名义工资,P为价格水平,r为利率。 (1)假设价格和工资充分弹性,请给出总需求函数和总供给函数,均衡产出与均衡价格水平是多少? (2)如果政府购买支出G增加200,在价格和工资弹性的条件下,均衡的价格水平和产出会如何变动?
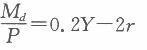
政府购买支出G=500短期总生产函数Y=20L劳动供给
劳动需求
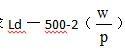
W为名义工资,P为价格水平,r为利率。 (1)假设价格和工资充分弹性,请给出总需求函数和总供给函数,均衡产出与均衡价格水平是多少? (2)如果政府购买支出G增加200,在价格和工资弹性的条件下,均衡的价格水平和产出会如何变动?
答案:
解析:
(1)产品市场的均衡条件为y=C+lJ-G,代人相关参数可得: Y=100+0. 8Y+1000-2r+500整理得IS曲线方程:Y=8 000-10r。 由货币市场均衡条件可得: =o.2Y -2r,此即为LM曲线方程。联立IS曲线方程和LM曲线方程可得总需求函数为:Y=4 000+ 。 联立劳动供给函数和劳动需求函数,解得:L=300。将L=300代入到生产函数,得Y=6 000,此为总供给函数。联立总供给函数和总需求函数,得:Y=6 000,P=l。 (2)当政府购买支出G增加200时,总供给函数和LM曲线方程不变。采用(1)计算方法,得出新的IS曲线方程为y=9 000 -10r,联立LM曲线方程可得此时的总需求函数为Y-4 500+ 生产。联立新的总需求函数和原有的总供给函数,解得:Y=6 000,P一号。这表明在充分就业的情况下,扩张性的财政政策只会使得价格上涨,而均衡产出保持不变。
第7题:
假设某商品需求函数为Q=100-2P,供给函数为Q=20+6P。 (1)该商品的市场均衡价格和销售量是多少? (2)如果政府对该商品征收每单位商品4元的数量税,市场均衡的销售量是多少?消费者支付的价格和生产商接受的价格分别是多少?税收负担如何分配? (3)如果商品供给函数变为Q= 40+6P,题目(1)和(2)中的答案该如何变化?
答案:
解析:
(1)联立需求函数和供给函数可得:100-2P=20+6P解得:均衡价格P=10。将P=10代入需求函数或供给函数可得销售量为80。 (2)如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足
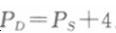
联立以下四个方程:
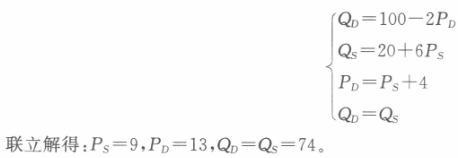
即市场均衡的销售量为74,消费者支付的价格为每单位13元,生产商接受的价格为每单位9元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 (3)联立需求函数和供给函数可得:100-2P=40+6P解得:均衡价格P=7.5。将P=7.5代入需求函数或供给函数可得销售量为85。如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足PD—PS+4。联立以下四个方程:
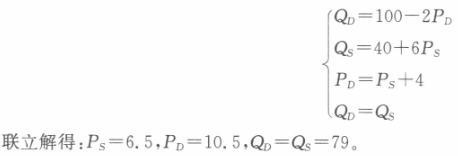
即市场均衡的销售量为79,消费者支付的价格为每单位10.5元,生产商接受的价格为每单位6.5元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 可以看出,由于供给曲线斜率不变,所以税负的转嫁程度不变,因为税负的转嫁程度取决于需求曲线和供给曲线的斜率。
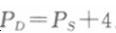
联立以下四个方程:
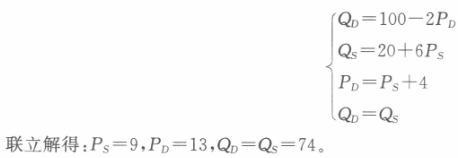
即市场均衡的销售量为74,消费者支付的价格为每单位13元,生产商接受的价格为每单位9元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 (3)联立需求函数和供给函数可得:100-2P=40+6P解得:均衡价格P=7.5。将P=7.5代入需求函数或供给函数可得销售量为85。如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足PD—PS+4。联立以下四个方程:
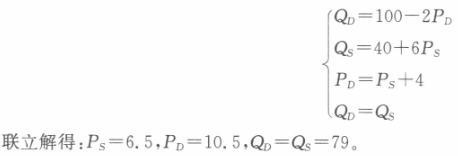
即市场均衡的销售量为79,消费者支付的价格为每单位10.5元,生产商接受的价格为每单位6.5元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 可以看出,由于供给曲线斜率不变,所以税负的转嫁程度不变,因为税负的转嫁程度取决于需求曲线和供给曲线的斜率。
第8题:
总供给函数为AS=2300+400P,总需求函数为AD=2000+4500/P。 试求: (1)均衡收入与均衡价格;
(2)总需求上升10%的均衡收入与均衡价格。
参考答案:已知:AS=2300+400P,AD=2000+4500/P
求均衡国民收入和均衡价格的公式为:AD=AS
2300+400P=2000+4500/P 4P+3P-45=0
根据:一元二次方程计算公式
P=3 Y=2300+400×3=3500 Y=2000+4500/3=3500
又已知:总需求上升10%
则:AD=2200+4950/P
2300+400P=2200+4950/P
2300P+400P2=2200P+4950
400P2+100P–4950=0
8P2+2P–99=0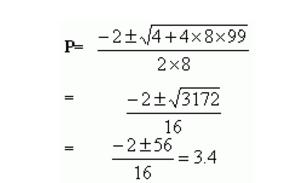
Y=2300+400×3.4=3660
Y=2000+4500/3.4=3324
求均衡国民收入和均衡价格的公式为:AD=AS
2300+400P=2000+4500/P 4P+3P-45=0
根据:一元二次方程计算公式
P=3 Y=2300+400×3=3500 Y=2000+4500/3=3500
又已知:总需求上升10%
则:AD=2200+4950/P
2300+400P=2200+4950/P
2300P+400P2=2200P+4950
400P2+100P–4950=0
8P2+2P–99=0
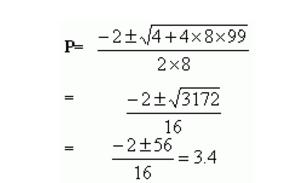
Y=2300+400×3.4=3660
Y=2000+4500/3.4=3324
第9题:
当某种商品的需求和供给出现同时减少的情况时,均衡价格和均衡数量的变化是( )。
A.均衡价格无法确定,均衡数量减少
B.均衡价格下降,均衡数量无法确定
C.均衡价格下降,均衡数量减少
D.均衡价格上升,均衡数量减少
B.均衡价格下降,均衡数量无法确定
C.均衡价格下降,均衡数量减少
D.均衡价格上升,均衡数量减少
答案:A
解析:
第10题:
当航空运输价格和供给不变时,若需求增加,则( )。
A.均衡价格和均衡数量减少
B.均衡价格和均衡数量反向变化
C.均衡价格和均衡数量增加
D.均衡价格和均衡数量不变
B.均衡价格和均衡数量反向变化
C.均衡价格和均衡数量增加
D.均衡价格和均衡数量不变
答案:C
解析:
如果供给不变,需求增加,则均衡价格和均衡数量也增加。
