设总体X服从分布N(0,2^2),而X1,X2,…,X15是来自总体X的简单随机样本,则随机变量服从_______分布,参数为________.
题目
设总体X服从分布N(0,2^2),而X1,X2,…,X15是来自总体X的简单随机样本,则随机变量 服从_______分布,参数为________.
服从_______分布,参数为________.
 服从_______分布,参数为________.
服从_______分布,参数为________.
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设(X1,X2,…,Xn)(N≥2)为标准正态总体X的简单随机样本,则().
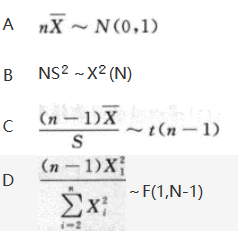
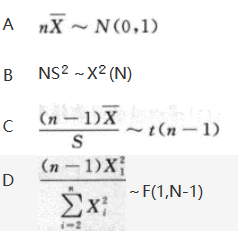
答案:D
解析: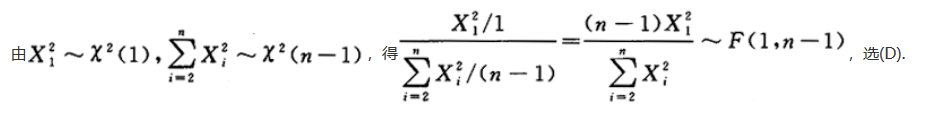
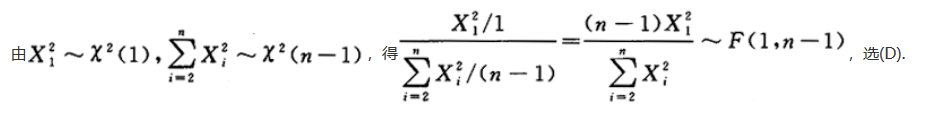
第2题:
设X1,X2,…,Xn,…为独立同分布的随机变量列,且均服从参数为λ(λ>1)的指数分布,记φ(x)为标准正态分布函数,则
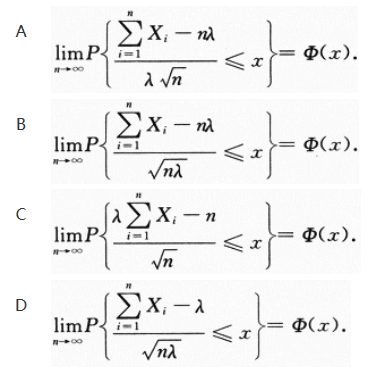

答案:C
解析:
【简解】本题是数四的考题.X1,X2,…,Xn,…独立同分布、方差存在.根据中心极限定理 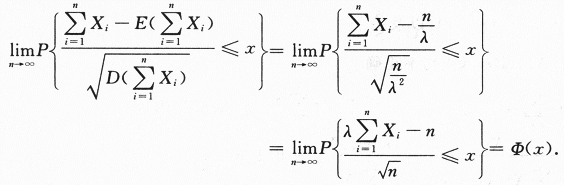
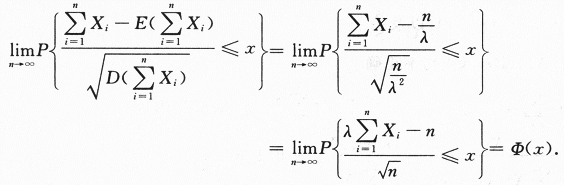
第3题:
设X1,X2,…,X16是来自总体X~N(4,б2)的简单随机样本,б2已知,令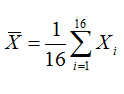 ,则统计量
,则统计量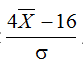 服从的概率密度函数为()
服从的概率密度函数为()
参考答案:

第4题:
设总体X的分布函数为
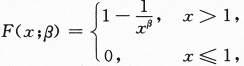
其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求:
(Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.
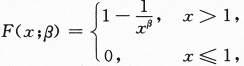
其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求:
(Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.
答案:
解析:

第5题:
设总体X在区间(0,θ)内服从均匀分布,X1,X2,X3是来自总体的简单随机样本.证明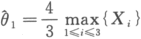 :与
:与 都是参数θ的无偏估计量,试比较其有效性.
都是参数θ的无偏估计量,试比较其有效性.
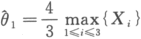 :与
:与 都是参数θ的无偏估计量,试比较其有效性.
都是参数θ的无偏估计量,试比较其有效性.答案:
解析:
【证明】因为总体X在区间(0,θ)内服从均匀分布,所以分布函数为




第6题:
设(X1,X2,X3)为来自总体X的简单随机样本,则下列不是统计量的是().


答案:B
解析:
因为统计量为样本的无参函数,故选(B).
第7题:
设总体X服从参数λ的指数分布,X1,X2,…,Xn是从中抽取的样本,则E(X)为( )。


答案:A
解析:
由于x服从指数分布,即

所以
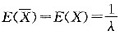

所以
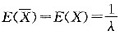
第8题:
设(X1,X2,…,Xn)是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知,则下列各项中,不是统计量的有( )。

正确答案:DE
解析:统计量中不含有任何未知参数,故D、E项不是统计量。
解析:统计量中不含有任何未知参数,故D、E项不是统计量。
第9题:
设总体X服从参数为2的指数分布,X1,X2,…,Xn为来自总体X的简单随机样本,则当n→∞时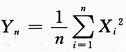 ,依概率收敛于_______.
,依概率收敛于_______.
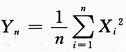 ,依概率收敛于_______.
,依概率收敛于_______.答案:
解析:
本题是数三的考题,根据切比雪夫大数定律或者辛钦大数定律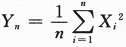 ,依概率收敛于
,依概率收敛于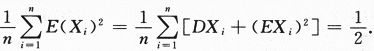 答案应填
答案应填
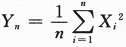 ,依概率收敛于
,依概率收敛于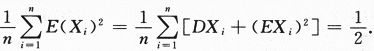 答案应填
答案应填
第10题:
设总体X~N(0,σ^2),X1,X2,…,X20是总体X的简单样本,求统计量U=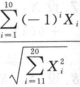 所服从的分布.
所服从的分布.
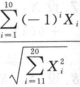 所服从的分布.
所服从的分布.答案:
解析:

