研究生入学
设总体X的密度函数为f(x)=,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
题目
设总体X的密度函数为f(x)=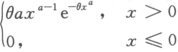
,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
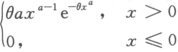,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设总体X的概率密度为
未知参数，X1,X2, ...Xn是来自总体X的样本，则θ的矩估计量是：
未知参数，X1,X2, ...Xn是来自总体X的样本，则θ的矩估计量是：
答案：B
解析：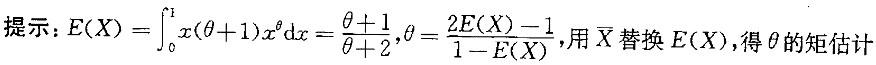
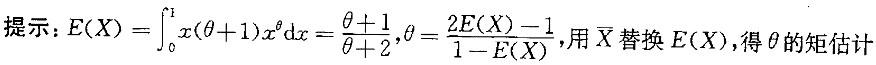
第2题：
设总体X的概率密度为f(x)=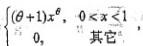
其中θ＞-1是未知参数，X1，X2，...Xn是来自总体X的样本，则θ的矩估计量是：
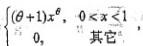其中θ＞-1是未知参数，X1，X2，...Xn是来自总体X的样本，则θ的矩估计量是：
答案：B
解析：
X的数学期望
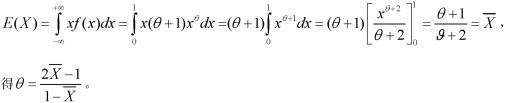
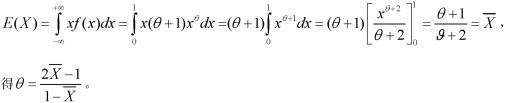
第3题：
已知总体X服从参数为λ的指数分布,设X1,X2,…,Xn是子样观察值,求λ的极大似然估计。
参考答案：
第4题：
设总体X的密度函数为f(x)=
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.答案：
解析：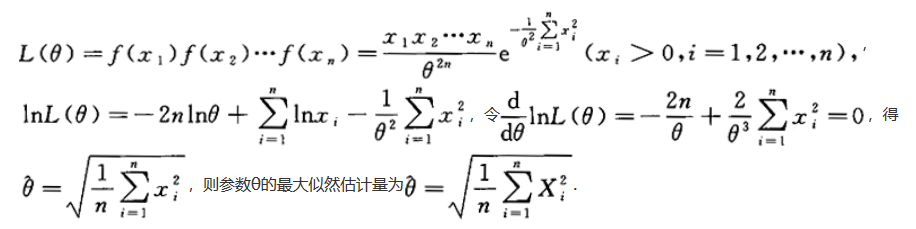
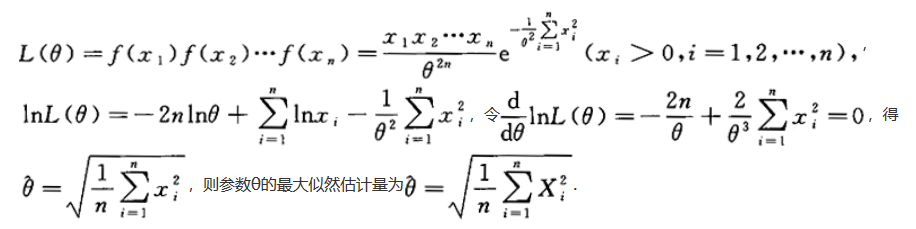
第5题：
设总体X的分布函数为
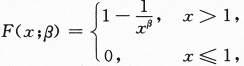
其中未知参数β>1，X1，X2，…，Xn为来自总体X的简单随机样本，求：
(Ⅰ)β的矩估计量；(Ⅱ)β的最大似然估计量.
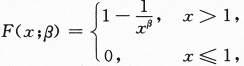
其中未知参数β>1，X1，X2，…，Xn为来自总体X的简单随机样本，求：
(Ⅰ)β的矩估计量；(Ⅱ)β的最大似然估计量.
答案：
解析：
第6题：
设总体X的概率密度为
而x1,x2,...,xn 是来自总体的样本值，则未知参数θ的最大似然估计值是:
而x1,x2,...,xn 是来自总体的样本值，则未知参数θ的最大似然估计值是:
答案：C
解析：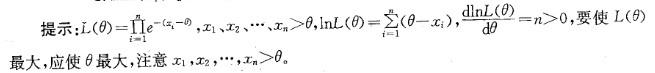
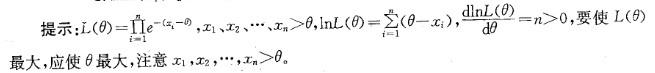
第7题：
设某元件的使用寿命X的概率密度为f(x；θ)=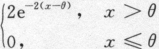
,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
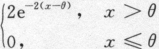,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.答案：
解析：
第8题：
设总体X服从参数为λ的泊松分布，其中λ未知.X1，…，Xn是取自总体X的样本，则λ的最大似然估计是( ).
A.
B.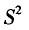
C.S
D.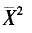
B.
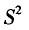
C.S
D.
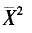
答案：A
解析：
第9题：
设总体X的分布律为P（X=k)
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.答案：
解析：
第10题：
设总体X的密度函数为f(x)=
,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ；(2)求D(θ).
,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ；(2)求D(θ).答案：
解析：