设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。A.I123 B. I132 C. I321 D. I312
题目
设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。
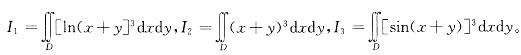
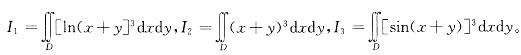
A.I123
B. I132
C. I321
D. I312
B. I132
C. I321
D. I312
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设平面区域D由曲线y=1/x及直线y=0,x=1,x=е2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)的联合密度函数为()。
参考答案:

第2题:
以下选项错误的是
A.main()
{ int x,y,z;
x=0;y=x-1;
z=x+y;}
B.main()
{ int x,y,z;
x=0,y=x+1;
z=x+y;}
C.main()
{ int x;int
int y;
x=0,y=x+1;
z=x+y;}
D.main()
{ int x,y,z;
x=0;y=x+1;
z=x+y,}
正确答案:D
第3题:
设(X,Y)服从在区域D上的均匀分布,其中D为x轴、y轴及x+y=1所围成,求X与Y的协方差Cov(X,Y).
正确答案:


第4题:
设平面闭区域D由x=0,y=0,x+y=1/2,x+y=1 所围成。
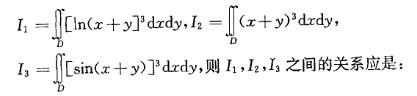
A.I123 B. I132
C. I321 D. I312
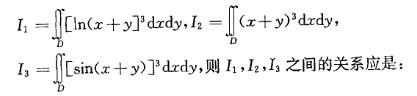
A.I123 B. I132
C. I321 D. I312
答案:B
解析:
提示:为了观察方便,做出平面区域D的图形,区域D在直线x+y=1的下方,在直线x+y=1/2上方以及由直线x= 0,y = 0围成。积分区域D上的点满足1/2≤x+y≤1。
故ln(x+y) ≤0,[ln(x+y)]3 ≤0
由三角函数知识,当0故033
所以平面区域D上的点满足:
[ln(x+y)]33 3
由二重积分性质:
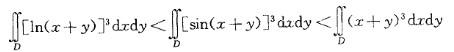
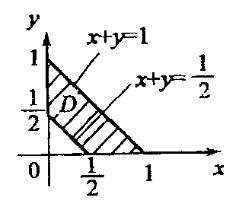
故ln(x+y) ≤0,[ln(x+y)]3 ≤0
由三角函数知识,当0故033
所以平面区域D上的点满足:
[ln(x+y)]33 3
由二重积分性质:
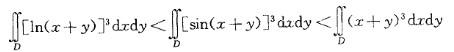

第5题:
设随机变量X,Y相互独立,X~U(0,2),Y~E(1),则.P(X+Y>1)等于().


答案:A
解析: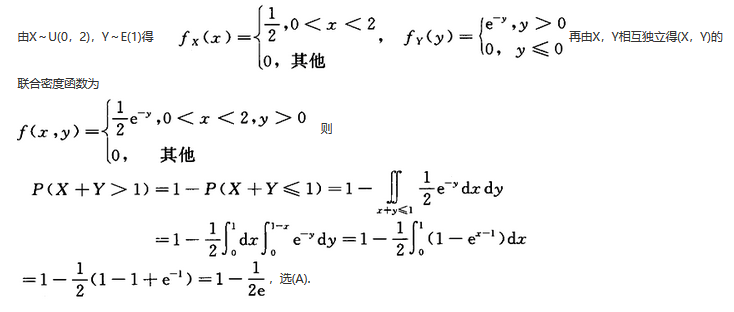
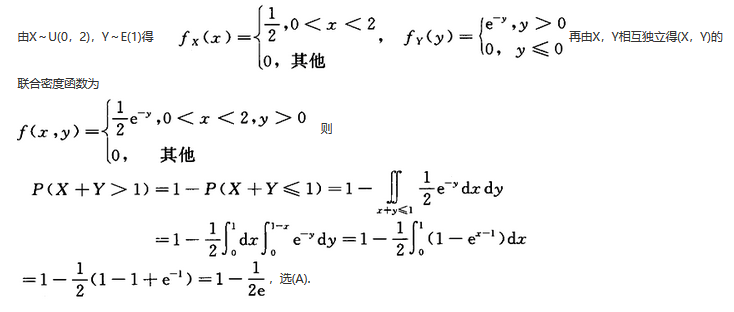
第6题:
设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X+Y服从的分布为()
A、X+Y服从N(0,1)
B、X+Y不服从正态分布
C、X+Y~X2(2)
D、X+Y也服从正态分布
参考答案:D
第7题:
平面上由条件X≥0、Y≥O和X+Y≤1所限定的区域,其面积为( ) 。
A.1/2
B.1
C.2
D.3
正确答案:A
本题考查应用数学基础知识。条件X0、Y0表示在第一象限,X+Y=1是连接(0,1)和(1,0)两点的直线。X+Y≤1是X+Y=I直线下方的区域。因此,在第一象限内,符合X+Y≤1的区域是个等腰直角三角形。两条直角边长都是1,因此面积为1/2。
本题考查应用数学基础知识。条件X0、Y0表示在第一象限,X+Y=1是连接(0,1)和(1,0)两点的直线。X+Y≤1是X+Y=I直线下方的区域。因此,在第一象限内,符合X+Y≤1的区域是个等腰直角三角形。两条直角边长都是1,因此面积为1/2。
第8题:
相互独立的随机变量X和Y都服从正态分布N(1,1),则()
A、P(X+Y≤0)=1/2
B、P(X-Y≤0)=1/2
C、P(X+Y≤1)=1/2
D、P(X-Y≤1)=1/2
参考答案:B
第9题:
下列( )项是在D={(x,y)|x2+y2≤1,x≥0,y≥0)上的连续函数f(x,y),且f(x,y)=3(x+y)+16xy。
A.f(x,y)=3(x+y)+32xy
B.f(x,y)=3(x+y)-32xy
C.f(x,y)=3(x+y)-16xy
D.f(x,y)=3(x+y)+16xy
B.f(x,y)=3(x+y)-32xy
C.f(x,y)=3(x+y)-16xy
D.f(x,y)=3(x+y)+16xy
答案:B
解析:
解本题的关键在于搞清二重积分
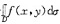
是表示一个常数,对f(x,y)=3(x+y)+

利用极坐标进行二重积分计算
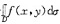
是表示一个常数,对f(x,y)=3(x+y)+

利用极坐标进行二重积分计算
第10题:
D 域由 x 轴,x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成, f (x, y)是连续函数,化
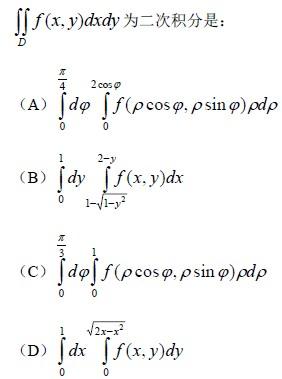
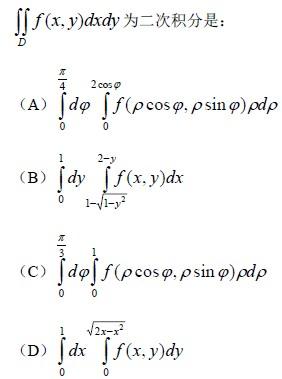
答案:B
解析:
解:选 B。
画积分区域如下图所示,
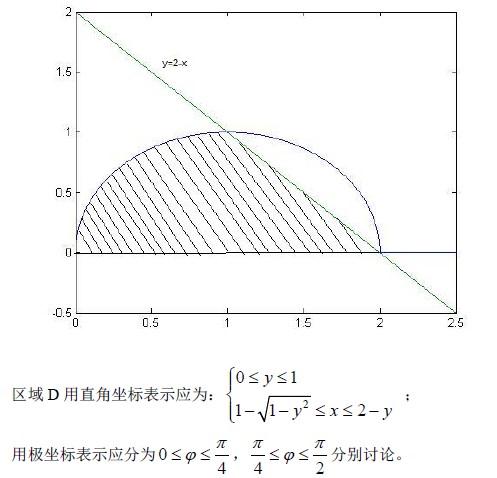
画积分区域如下图所示,

