对于一般正态分布,如X~N(1,4),则有关该正态分布的概率密度曲线的叙述不正确的是()。A、该分布的概率密度函数曲线关于x=1对称B、在x=1处达到最大值C、x轴为渐近线D、该概率密度函数曲线关于y轴对称
题目
对于一般正态分布,如X~N(1,4),则有关该正态分布的概率密度曲线的叙述不正确的是()。
- A、该分布的概率密度函数曲线关于x=1对称
- B、在x=1处达到最大值
- C、x轴为渐近线
- D、该概率密度函数曲线关于y轴对称
相似问题和答案
第1题:
A、正态分布以均值μ为中心,左右对称。曲线下面积集中在中心部分,越远离中心。曲线越接近横轴
B、正态分布中的X取值范围理论上没有边界(-∞<X<∞),X越远离μ。函数值f(X)越接近,但不会等于0
C、正态分布曲线由2个参数μ和σ决定。是变异参数,决定分布曲线的形态,σ是位置(即平均水平)参数,决定分布曲线在横轴的偏移位置
D、正态分布曲线下的面积分布有一定的规律。所有正态分布曲线,在μ左右的任意个标准差范围内面积相同
第2题:
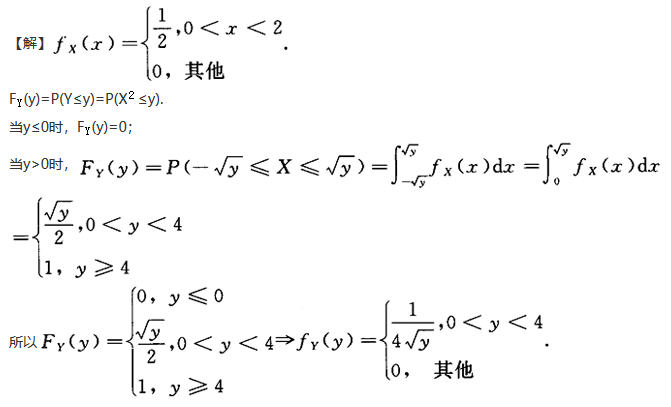
第3题:
关于概率密度函数p(x),应强调的是( )。
A.对应图上的纵轴原是“单位长度上的频率”,由于频率的稳定性,可用概率代替频率,从而纵轴就成为“单位长度上的概率”
B.它最后形成的曲线是概率曲线
C.它最后形成的曲线可位于X轴的上方,也可位于X轴下方
D.曲线与X轴所夹面积小于等于1
解析:对于概率密度函数p(x)应强调的是:图上的纵轴原是“单位长度上的频率”,由于频率的稳定性,可用概率代替频率,从而纵轴就成为“单位长度上的概率”,即概率密度,最后形成的曲线称为概率密度曲线。概率密度曲线一定位于x轴的上方,它与x轴围成面积恰好为1。
第4题:
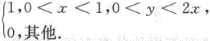 求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.
求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.
第5题:
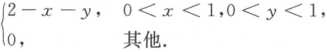 (1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
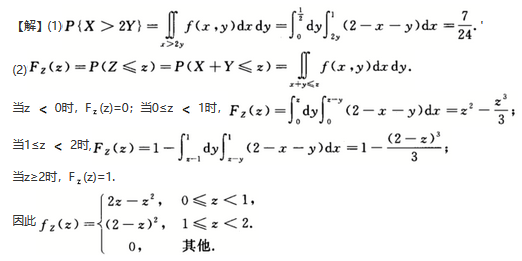
第6题:
已知(X,Y)服从均匀分布,联合概率密度函数为

设Z=max{X,Y}求Z的概率密度函数fz(z)
答案:X与Y都服从(0, 1)上的均匀分布,则fx与fy在(0, 1)上恒等于1。
Z = z <==> {X = z && Y <= z} + {Y = z && X < z}
因此,fz(z)dz = fx(z)dz * Integrate[fy(z)dy, (0, z)] + fy(z)dz * Integrate[fx(z)dx, (0, z)]
fz(z)dz = zdz + zdz = 2zdz
故fz(z) = 2z,z属于(0, 1).
第7题:
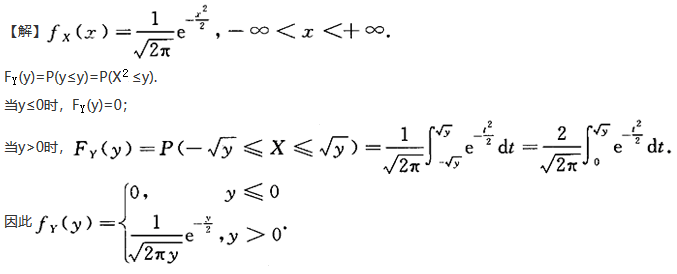
第8题:
下列关于正态分布曲线描述不正确的是( )。
A.正态分布曲线关于直线x=μ对称
B.当x=μ时,曲线位于最高点
C.当x<μ时,曲线上升(增函数);当x>μ时,曲线下降(减函数)并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近
D.μ一定时,曲线的形状由σ确定,σ越大,曲线越“瘦高”,总体分布越集中;σ越小,曲线越“矮胖”,总体分布越分散
第9题:
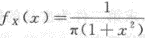 ,则y=2X的密度函数为
,则y=2X的密度函数为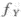 (y)=_______.
(y)=_______.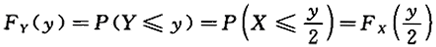 , 所以.
, 所以.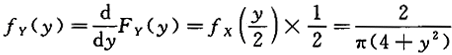
第10题:
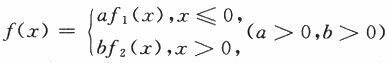 为概率密度,则a,b应满足
为概率密度,则a,b应满足B.3a+2b=4
C.a+b=1
D.a+b=2

