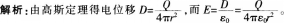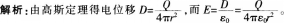带电量Q的导体A置于外半径为R的导体球壳B内,则球壳外离球心r处的电场强度大小(),球壳的电势()。
题目
带电量Q的导体A置于外半径为R的导体球壳B内,则球壳外离球心r处的电场强度大小(),球壳的电势()。
参考答案和解析
正确答案:E=Q/4πε0r2;V=Q/4πε0R
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
(本题8分)真空中有一个半径为R的孤立带电导体球,导体球表面附近的场强大小为E0,试求:
(1)导体球所带电量;
正确答案:
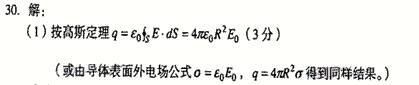
第2题:
无限大真空中一半径为a的带电导体球,所带体电荷在球内均匀分布,体电荷总量为q。在球外(即r a处)任一点r处的电场强度的大小E为( )V/m。


答案:D
解析:
解带电金属球在无限大均匀介质中产生的电场强度E=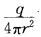 V/m。
V/m。
答案:D
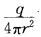 V/m。
V/m。
答案:D
第3题:
一半径为R的均匀带电球壳,在其球心O处放置一点电荷q,该电荷受的电场力为零,若该电荷偏离球心O,则该电荷q的受力情况为()。
A、变大
B、变小
C、不变
D、无法判断
参考答案:A
第4题:
如图4所示,一个未带电的空腔导体球壳,内半径为R,在腔内离球心的距离为d处(d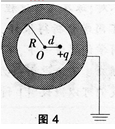



答案:D
解析:

第5题:
真空中有一均匀带电球表面,半径为R,电荷总量为q,则球心处的电场强度大小应为下列哪项数值?( )
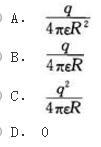
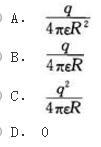
答案:D
解析:
带电球体中心场强为0,分析如下取中性点半径为r的小球,其场强为:
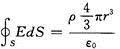
解得
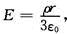
当 r→0时的极限,即电场强度E=0。
【说明】根据高斯定理,在任意闭合曲面上,电位移向量的面积积分恒等于该闭合曲面内所有自由电荷的代数和,已知带电球面的自由电荷只是分布在表面,内部没有自由电荷,因此球心处的电场强度为0。这种现象又称为静电屏蔽效应,带电球面的中心处电场强度为0。
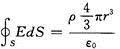
解得
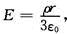
当 r→0时的极限,即电场强度E=0。
【说明】根据高斯定理,在任意闭合曲面上,电位移向量的面积积分恒等于该闭合曲面内所有自由电荷的代数和,已知带电球面的自由电荷只是分布在表面,内部没有自由电荷,因此球心处的电场强度为0。这种现象又称为静电屏蔽效应,带电球面的中心处电场强度为0。
第6题:
已知一带电量为q=10-6C 的点电荷距离不接地金属球壳(其半径R= 5cm)的球心1.5cm处,则球壳表面的最大电场强度Emax为()。
A. 2.00X104V/m B. 2.46X106V/m
C. 3.6X106V/m D. 3.23X106V/m
A. 2.00X104V/m B. 2.46X106V/m
C. 3.6X106V/m D. 3.23X106V/m
答案:C
解析:
解球壳外部的电场相当于将点电荷置于球心时的电场强度:


第7题:
在无限大真空中,有一半径为α的导体球,离球心d(d>α)处有一点电荷q ,该导体球的电位ψ应为下列哪项数值?( )


答案:A
解析:

第8题:
一导体球壳带电为Q,在球心处放置电量q,静电平衡后,内表面的电量为-q。()
此题为判断题(对,错)。
参考答案:正确
第9题:
-深埋地下的导体球,球的半径为R,土壤电导率为g,其接地电阻为( )。
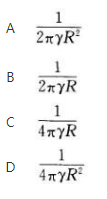
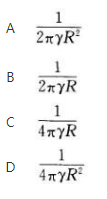
答案:C
解析: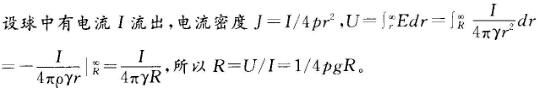
第10题:
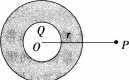
如图,在一带电量为Q的导体球外,同心地包有一各向同性均匀电介质球壳,其相对电容率为εr,,壳外是真空,则在壳外P点处(OP=r)的场强和电位移的大小分别为( )。
A.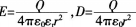
B.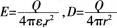
C.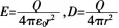
D.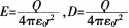

A.
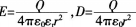
B.
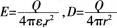
C.
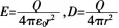
D.
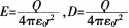
答案:C
解析: