军队文职招聘考试
设经济的总供给函数为y=2350+400P，总需求函数为y=2000+750/P，求总供给和总需求：均衡时的收入和价格水平。
题目
设经济的总供给函数为y=2350+400P，总需求函数为y=2000+750/P，求总供给和总需求：均衡时的收入和价格水平。
参考答案和解析
y=2350+400P
y=2000+750/P
易得均衡时的价格和收入分别为P=1和y=2750。
相似问题和答案
第1题：
假定经济由四部门构成：Y=C+I+G+NX，其中消费函数为C=300+0.8Yd(Yd为可支配收入)，投资函数为I=200-1500r(r为利率)，政府支出为G=200，利率t=0.2，进出口函数为NX=100-0.04Y-500r，实际货币需求函数L=0.5Y-2000r，名义货币供给M=550，那么IS方程与总需求函数分别为( )。
A．Y=2000-5000r
B．Y=1500-5000r
C．0.5Y-2000r=550/P
D．
E．
解析：根据题意有：Y=C+IG+NX=300+0.8×(Y-0.2Y)+200-1500r+200+100-0.04Y-500r=800+0.6Y-2000r解得：Y=2000-5000r，即为IS方程；由L=M/P，得0.5Y-2000r=550/P，即为LM方程。将两个方程联立，消去r，得：，此为总需求函数。
第2题：
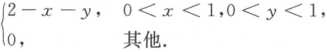(1)求P(X>2Y)；(2)设Z=X+Y,求Z的概率密度函数.
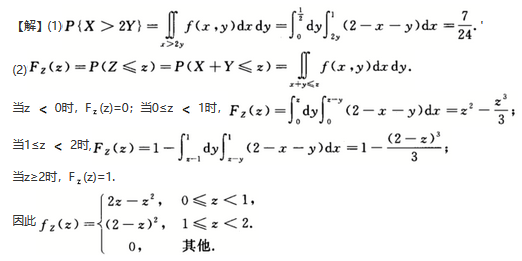
第3题：
A、0;
B、1;
C、Y的分布函数;
D、Y的密度函数。
第4题：
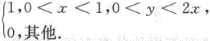求：(1)(X,Y)的边缘密度函数；(2)2=2X-Y的密度函数.
第5题：
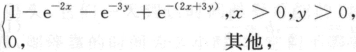则P(max{X,y}>1)=_______.
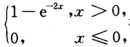得X～E(2)，同理Y～E(3)，且X,Y独立.P(max{X,Y}>1)=P(X>1Y>1)=1-P(X≤1,Y≤1)=1-P(X≤1)P(Y≤1)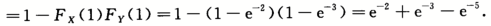
第6题：
=1-【1-P(X≤z)】【1-P(Y≤z)】=1-【1-FX(z)】【1-FY(z)】，选(C).
第7题：
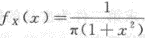,则y=2X的密度函数为
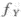(y)=_______.
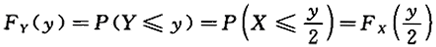， 所以.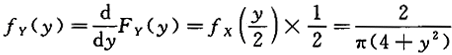
第8题：
计算分析题：设消费函数C=100+0.75Y,投资函数I=20-2r，货币需求函数L=0.2Y-0.5r,货币供给M=50。价格水平为P。求：（1）总需求函数；（2）当价格为10和5时的总需求；（3）政府购买增加50时的总需求曲线并计算价格为10和5时的总需求；（4）货币供给增加20时的总需求函数。
（1）由Y＝C＋I得ＩＳ曲线：r=60-1/8Y
由M／P＝L得LM曲线：r=-100/P+0.4Y
联立两式得总需求曲线：Y=190/P+114.
（2）根据（1）的结果可知：P＝10时，＝133；P＝5时，Y＝152。
（3）由Y＝C＋I＋G得：Y=190/P+162
P=10,Y=181;P=5,Y=200。
（4）LM曲线为：r=0.4Y-140/P，再结合ＩＳ曲线r=60-1/8Y，得：Y=267/P+114
第9题：
,Fy(y)=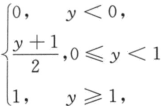
,令U=X+Y,则U的分布函数为_______.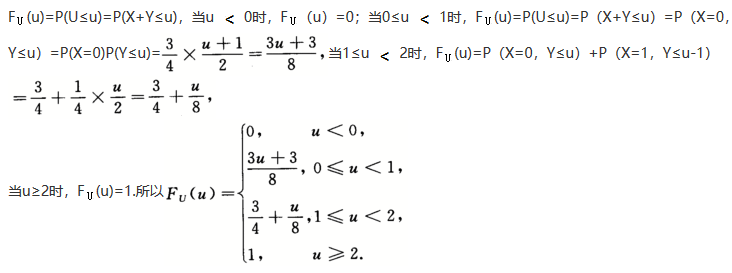
第10题：