令要素L的价格为w,要素K的价格为r。那么,只组合要素L和K(以L为横轴)得到的等成本线的斜率是()A、w/rB、r/wC、Kr/LwD、Lw/Kr
题目
令要素L的价格为w,要素K的价格为r。那么,只组合要素L和K(以L为横轴)得到的等成本线的斜率是()
- A、w/r
- B、r/w
- C、Kr/Lw
- D、Lw/Kr
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
等成本线斜率的决定因素有()。
A. 劳动投入L的价格
B. 资本投入要素K的价格
C. 劳动和资本要素价格之比
D. 总成本变化
标准答案:ABC
第2题:
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。假设企业处在长期生产中,w=1,v=4, 企业的最优生产方式是什么?企业的长期成本函数是什么?
答案:
解析:

第3题:
已知某企业的生产函数Q=L2/3K1/3 ,劳动的价格W=2,资本的价格r=1,
求:
(1)当成本C=3000时,企业实现最大产量时的L、K和Q的值。
(2)当产量Q=800时,企业实现最少成本时的L、K和C的值。
参考答案:
如图:
L=800K=800 C=2L+K=3×800=2400
第4题:
假设厂商的生产函数为
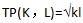
要素K、L价格分别为
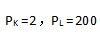
两种要素的投入数量均可以调整。 (1)计算总成本TC(Q)。 (2)若该厂商在产品市场是完全垄断者,且该市场需求曲线是P=2 000-100Q,计算垄断价格。
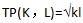
要素K、L价格分别为
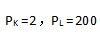
两种要素的投入数量均可以调整。 (1)计算总成本TC(Q)。 (2)若该厂商在产品市场是完全垄断者,且该市场需求曲线是P=2 000-100Q,计算垄断价格。
答案:
解析:

第5题:
已知一个厂商的生产函数Q=1/11(4KL - L2一K2),其中K和L分别表示资本和劳动,且要素市场价格分别为v和ω。产品的市场价格为P,而该企业仅是一个价格接受者。 该企业现有资本存量为

当面临短期的产品价格波动时,它将如何生产?

当面临短期的产品价格波动时,它将如何生产?
答案:
解析:
对于该企业而言,利润函数为:π=PQ-vK-ωL 在短期,当资本存量一定时,厂商的利润函数为:

企业利润最大化的一阶条件为:
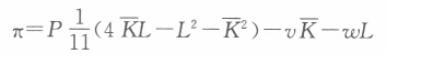
此时,企业所需要的劳动力为
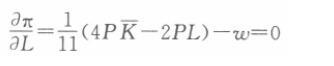

企业利润最大化的一阶条件为:
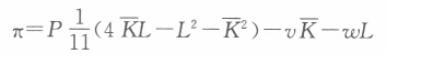
此时,企业所需要的劳动力为
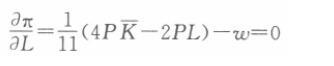
第6题:
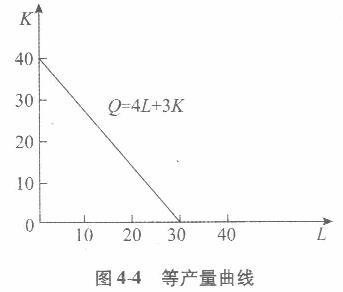
已知某厂商使用L和K两种要素生产一种产品,其固定替代比例的生产函数为Q=4L+3K (1)作出等产量曲线。 (2)边际技术替代率是多少? (3)讨论其规模报酬情况。 (4)令PL=5、PK =3,求C=90时的K、L值以及最大产量。 (5)令PL =3、PK =3,求C=90时的K、L值以及最大产量。 (6)令PL =4、PK =3,求C=90时的K、L值以及最大产量。 (7)比较(4)、(5)和(6),你得到什么结论?
答案:
解析:
(1)如图44所示。

故此时全部使用要素L,即K=O,L=30。 (6)由题可知MRTSLK=PL/PK 此时使用L与K要素均可(只需满足约束条件)。 (7)比较(4)、(5)和(6)可以得到一般的结论: 1)对于固定比例生产函数而言,如果等产量曲线斜率的绝对值小于预算线斜率的绝对值,则厂商的均衡点位于等产量曲线与预算线在纵轴的交点。 2)如果等产量曲线斜率的绝对值大于预算线斜率的绝对值,则厂商生产的均衡点位于等产量曲线与预算线在横轴的交点,在以上两种情况下,厂商只使用一种要素进行生产,另一种要素使用量为零。 3)如果等产量曲线斜率的绝对值等于预算线斜率的绝对值,即两线重合,则厂商生产的均衡点可以发生在该重合线上的任意位置,只需满足预算约束条件即可。


故此时全部使用要素L,即K=O,L=30。 (6)由题可知MRTSLK=PL/PK 此时使用L与K要素均可(只需满足约束条件)。 (7)比较(4)、(5)和(6)可以得到一般的结论: 1)对于固定比例生产函数而言,如果等产量曲线斜率的绝对值小于预算线斜率的绝对值,则厂商的均衡点位于等产量曲线与预算线在纵轴的交点。 2)如果等产量曲线斜率的绝对值大于预算线斜率的绝对值,则厂商生产的均衡点位于等产量曲线与预算线在横轴的交点,在以上两种情况下,厂商只使用一种要素进行生产,另一种要素使用量为零。 3)如果等产量曲线斜率的绝对值等于预算线斜率的绝对值,即两线重合,则厂商生产的均衡点可以发生在该重合线上的任意位置,只需满足预算约束条件即可。
第7题:
假设一家企业的生产函数是f(K,L) = K2L2,其中L的价格是w,K的价格是r,请回答以下问题: (1)证明企业的生产技术是规模报酬递增的。 (2)长期扩展路径(long- run expansion path)是由资本和劳动最优组合所组成的曲线,请用画图的方法把这一路径找出来。 (3)如果w=10、r=2,请找出这条长期扩展路径具体的函数形式。
答案:
解析:
(1)当L和K均扩大t倍(t>1)时,则有:
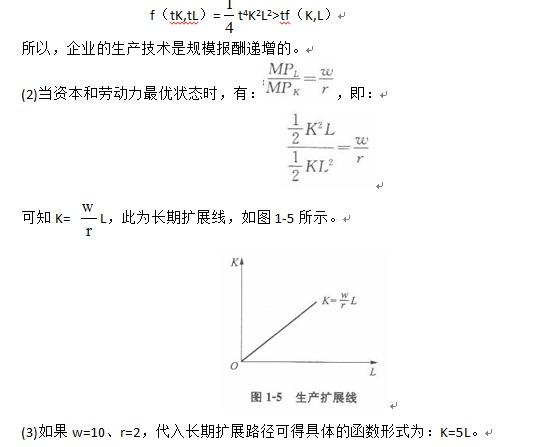

第8题:
当生产要素L的市场供给曲线(SL)斜率为正时()。
A、不论该要素价格PL如何,该要素的供给量总是固定的
B、其需求曲线单独决定均衡价格
C、该要素的需求曲线与供给曲线之交点决定均衡价格,而不决定均衡数量
D、该要素的需求曲线与供给曲线之交点决定均衡价格和均衡数量
参考答案:D
第9题:
假定一个竞争性厂商,其生产函数为Q=f(L,K)=AL^αK^β,生产要素L和K的价格分别为w和r。 (1)试求在K为不变投入时厂商的短期成本函数。 (2)求厂商的长期成本函数,并讨论不同的规模报酬对平均成本曲线形状的影响。
答案:
解析:

第10题:
已知某厂商的固定投入比例的生产函数为Q=min{2L,3K} (1)令PL =1、PK =3,求厂商为了生产120单位产量所使用的K、L值以及最小成本。如果要素价格变化为PL =4、PK =2,厂商为了生产120单位产量所使用的K、L值以及最小成本又是多少?请予以比较与说明。 (2)令PL =4、PK =3,求C=180时的K、L值以及最大产量。
答案:
解析:
(1)由题意可知,当固定投入比例生产要素为最佳组合时,Q=2L=3K。 Q =120时,1= 60,K=40。 当PL =1、PK =3时,成本C=PL·L+PK·K=180; 当PL =4、PK =2时,成本C=PL·L+PK·K=320。 比较两个结果可知,第二种价格的成本更高,因为投入比例固定,L投入比K投入数量多,L价格越高成本越高。 (2)由题意可知,C=PL.L+PK·K。 C= 180,PL=4,PK =3,即4L+3K= 1800 (1) 又由(1)得Q=2L=3K, (2) 联立可得L=30,K=20,此时Q=60。
