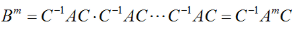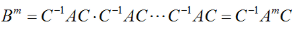理学
问答题设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。
题目
问答题
设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。
参考答案和解析
正确答案：
因为A非奇异，U的对角元uii不为零，又LU分解等价于高斯消去法，aii（i）=uii≠0由引理可知，矩阵A的顺序主子式均不为零。
解析：
暂无解析
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
若把A分解成一个下三角阵L和一个单位上三角阵U的乘积，称为克洛特(Crout)分解。()
参考答案：正确
第2题：
设A为n阶实对称矩阵,下列结论不正确的是().
A.矩阵A与单位矩阵E合同
B.矩阵A的特征值都是实数
C.存在可逆矩阵P,使P^-1AP为对角阵
D.存在正交阵Q,使Q^TAQ为对角阵
B.矩阵A的特征值都是实数
C.存在可逆矩阵P,使P^-1AP为对角阵
D.存在正交阵Q,使Q^TAQ为对角阵
答案：A
解析：
根据实对称矩阵的性质，显然(B)、(C)、(D)都是正确的，但实对称矩阵不一定是正定矩阵，所以A不一定与单位矩阵合同，选(A).
第3题：
n阶对称矩阵A正定的充分必要条件是()。
A、|A|0
B、存在n阶方阵C使A=CTC
C、负惯性指标为零
D、各阶顺序主子式均为正数
参考答案：D
第4题：
设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵
.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.
.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.答案：
解析：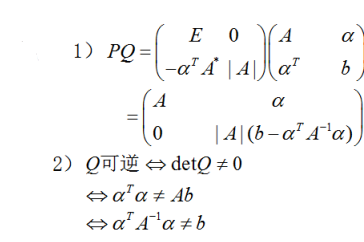
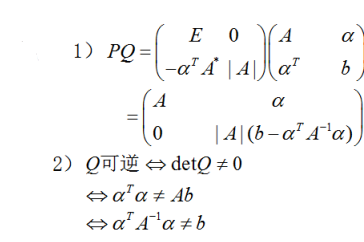
第5题：
设A为n阶矩阵，则A以零为其特征值是A为奇异矩阵(即 A =0)的:
A.充分非必要条件
B.必要非充分条件
C.既非充分也非必要条件
D.充分必要条件
A.充分非必要条件
B.必要非充分条件
C.既非充分也非必要条件
D.充分必要条件
答案：D
解析：
提示:可通过下面证明说明。充分性:若矩阵A有特征值0→矩阵A奇异(即 A =0)，若λ=0为矩阵A的特征值，则存在非零向量a，使Aa=0a，Aa=0，即齐次线性方程组Ax =0有非零解，故 A =0，故矩阵A为奇异矩阵。
必要性:若矩阵A是奇异矩阵，即 A =0→λ=0是矩阵A的特征值，已知A是奇异矩阵， A =0，取λ=0，有 A-λE = A-0E= A =0，λ=0，满足特征方程 A-λE =0，故λ=0 是矩阵A的特征值。
必要性:若矩阵A是奇异矩阵，即 A =0→λ=0是矩阵A的特征值，已知A是奇异矩阵， A =0，取λ=0，有 A-λE = A-0E= A =0，λ=0，满足特征方程 A-λE =0，故λ=0 是矩阵A的特征值。
第6题：
将非奇异阵A分解成一个下三角阵L和一个上三角阵U的乘积：A=LU称为对矩阵A的三角分解。()
参考答案：正确
第7题：
下列结论中正确的是（ ）。
A、 矩阵A的行秩与列秩可以不等
B、 秩为r的矩阵中，所有r阶子式均不为零
C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
D、 秩为r的矩阵中，不存在等于零的r-1阶子式
B、 秩为r的矩阵中，所有r阶子式均不为零
C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
D、 秩为r的矩阵中，不存在等于零的r-1阶子式
答案：C
解析：
A项，矩阵A的行秩与列秩一定相等。B项，由矩阵秩的定义可知，若矩阵A（m×n）中至少有一个r阶子式不等于零，且r＜min（m，n）时，A中所有的r+1阶子式全为零，则A的秩为r。即秩为r的矩阵中，至少有一个r阶子式不等于零，不必满足所有r阶子式均不为零。C项，矩阵A的行列式不等于零意味着矩阵A不满秩，n阶矩阵的秩为n时，所对应的行列式的值大于零；当n阶矩阵的秩＜n时，所对应的行列式的值等于零。D项，秩为r的矩阵中，有可能存在等于零的r-1阶子式，如秩为2的矩阵
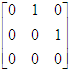
中存在等于0的1阶子式。
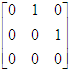
中存在等于0的1阶子式。
第8题：
设A为m*n矩阵,则有()。
A、若mn，则有ax=b无穷多解
B、若mn，则有ax=0非零解，且基础解系含有n-m个线性无关解向量;
C、若A有n阶子式不为零，则Ax=b有唯一解;
D、若A有n阶子式不为零，则Ax=0仅有零解。
参考答案：D
第9题：
设A是nxm矩阵，B是mxn矩阵，E是n阶单位阵，若AB=E，证明B的列向量组线性无关。
答案：
解析：
第10题：
设A、B、C为同阶矩阵，且C为非奇异矩阵，满足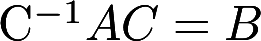
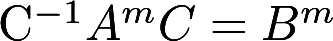
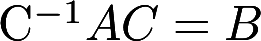，求证：
，求证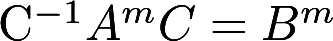：答案：
解析：