专业科目
单选题设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx（ ）。A ln[（2x－1）/（x＋1）]（x＋1）B ln[（2x－1）/（x＋1）]/（x＋1）2C ln[（2x－1）/（x＋1）]（x＋1）2D ln[（2x－1）/（x＋1）]/（x＋1）
题目
单选题
设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx（ ）。
A
ln[（2x－1）/（x＋1）]（x＋1）
B
ln[（2x－1）/（x＋1）]/（x＋1）2
C
ln[（2x－1）/（x＋1）]（x＋1）2
D
ln[（2x－1）/（x＋1）]/（x＋1）
参考答案和解析
正确答案：
D
解析：
令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。
令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设y=f(t)，t=φ(x)都可微，则dy=( )。
A.f′(t)dt
B.φ′(x)dx
C.f′(t)φ′(x)dt
D.f′(t)dx
B.φ′(x)dx
C.f′(t)φ′(x)dt
D.f′(t)dx
答案：A
解析：
第2题：
若函数z=ln(xy)/y,则当x=e,y=e-1时，全微分dz等于（ ）。
A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy
A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy
答案：C
解析：
正确答案是C。
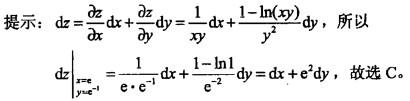
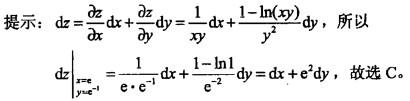
第3题：
设f(x)=ln(x＋1),则f(f(x))的定义域是多少?
参考答案：f(f(x))=ln[ln(x+1)+1]
ln(x+1)+1>0
ln(x+1)>-1
x+1>1/e
x>1/e-1
第4题：
单选题
设函数f（u）可微，且f′（0）＝1/2，则z＝f（4x2－y2）在点（1，2）处的全微分dz|（1，2）＝（ ）。
A
4dx＋2dy
B
4dx－2dy
C
－4dx＋2dy
D
－4dx－2dy
正确答案：
A
解析：
求全微分，即需求出函数对各个自变量的偏导。令u＝4x2－y2，则∂z/∂x＝f′（u）·∂u/∂x＝f′（u）·8x，∂z/∂y＝f′（u）·∂u/∂y＝f′（u）·（－2y），将（1，2）代入u＝4x2－y2得u＝0，又f′（0）＝1/2，故dz|（1，2）＝f′（0）·8dx＋f′（0）·（－2·2）dy＝4dx－2dy。
求全微分，即需求出函数对各个自变量的偏导。令u＝4x2－y2，则∂z/∂x＝f′（u）·∂u/∂x＝f′（u）·8x，∂z/∂y＝f′（u）·∂u/∂y＝f′（u）·（－2y），将（1，2）代入u＝4x2－y2得u＝0，又f′（0）＝1/2，故dz|（1，2）＝f′（0）·8dx＋f′（0）·（－2·2）dy＝4dx－2dy。
第5题：
填空题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。
正确答案：
-1/7
解析：
由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。
由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。
第6题：
设参数方程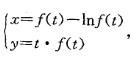
确定了y是x的函数，且f(t)存在，f(0) = 2，
f(0) = 2，则当t=0时，dy/dx的值等于：
A. 4/3 B. -4/3 C. -2 D. 2
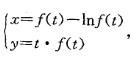确定了y是x的函数，且f(t)存在，f(0) = 2，
f(0) = 2，则当t=0时，dy/dx的值等于：
A. 4/3 B. -4/3 C. -2 D. 2
答案：C
解析：
提示:利用参数方程导数公式计算出dy/dx，代入t=0，得到t=0时的dy/dx值。计算如下：
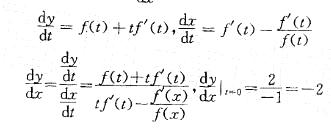
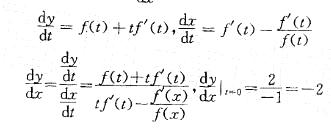
第7题：
设y=f（t），t=φ（x）都可微，则dy=（）。
- A、f＇（t）dt
- B、φ＇（x）dx
- C、f＇（t）φ＇（x）dt
- D、f＇（t）dx
正确答案:A
第8题：
设函数f(x)=1／x＋1,则f(f(x))=()。
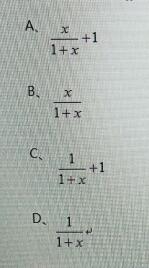
答案：A
解析：由函数f(x)=1/x+1，
令f(x)=t
则f(f(x))=f(t)=1/t+1=1/(1/x+1)+1=x/(1+x)+1，故选A。
第9题：
单选题
设y＝f（lnx）ef（x），其中f可微，则dy＝（ ）。
A
[f′（lnx）ef（x）＋f′（x）f（lnx）ef（x）]dx
B
[f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x）]dx
C
[f（lnx）ef（x）/x＋f（x）f（lnx）ef（x）]dx
D
[f′（lnx）ef（x）/x＋f（x）f（lnx）ef（x）]dx
正确答案：
B
解析：
由y′＝f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x），得dy＝[f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x）]dx。
由y′＝f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x），得dy＝[f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x）]dx。
第10题：
单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（ ）。
A
1
B
2
C
3
D
4
正确答案：
B
解析：
ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。