公路水运工程试验检测员

单选题某产品的批量N=10，不合格率P=0.3，抽检的方案为n=3，c=1时，合格的接收概率L（P）=（）。A 0.175B 0.291C 0.3D 0.466

题目
单选题
某产品的批量N=10，不合格率P=0.3，抽检的方案为n=3，c=1时，合格的接收概率L（P）=（）。
A

0.175

B

0.291

C

0.3

D

0.466

如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案

第1题：

某汽车零部件生产厂生产一批轴承，现要根据被检样本中的不合格产品数来推断是否接受整批产品，已知有两种计件抽样方案，方案甲为：n=10，Ac=0；方案乙为：n=20， Ac=0。请分析下列问题：

记甲方案的OC曲线为L甲(p)，则L甲(0.05)为( )。

A．0.951

B．0.959

C．0.95

D．1.00


正确答案：A
解析：

第2题：

批量N=10的产品，其中不合格品D=3，先从中抽取n=2个样品进行检查，求出现1个不合格品的概率?


正确答案：出现1个不合格品的概率为：　　1 2-1 2 1 1 2 P(1)= C3·C10-3/ C10 = C3·C7/ C10　　= 3*7/45=0.466　　答：出现1个不合格品的概率为0.466

第3题：

某类儿童玩具的不合格率为0.1，现用抽样方案(10，1)对多批产品进行抽检，已知每批产品的批量为N=1000，则：

接收概率L(p)约为( )。

A．0.5

B．0.74

C．0.81

D．0.90


正确答案：B
解析：

第4题：

抽样方案的接收概率随（ ）变化，形成抽样方案的OC曲线。
A.样本量n B.批量N C.批质量p D.生产方风险a


答案：C
解析：

第5题：

某汽车零部件生产厂生产一批轴承，现要根据被检样本中的不合格产品数来推断是否接受整批产品，已知有两种计件抽样方案，方案甲为：n = 10，Ac =0；方案乙为：n=20， Ac=0。请分析下列问题：
记甲方案的OC曲线为L甲(p)，则L甲(0.05)为（ ）。
A. 0. 9510 B. 0. 959 C. 0. 95 D. 1.00


答案：A
解析：

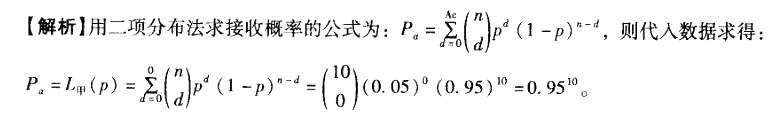
第6题：

批不合格品率p的公式是( )。

A．p=C/N

B．p=C/N×l00

C．P=D/N×l00

D．p=D/N


正确答案：D
解析：批不合格品率p等于批的不合格品数D除以批量N，即p=D/N。

第7题：

连续使用一次抽样方案（5，1)对产品批进行验收，若批量N= 1 000，批质量水平p= 10 (%)的接收概率L (0.1) =0.923 2,则平均检出质量约为（ ）。
A. 0. 092 32 B. 0. 046 16
C. 0.009 232 D. 0.184 64


答案：A
解析：
。AOQ=pL(p)。

第8题：

对一批产品进行检验，已知不合格品率P＝0.02。

批量N＝50，抽样方案为(10，0)，则拒收概率为( )。

A．0.10

B．0.90

C．0.99

D．0.01


正确答案：A
解析：(1)使用超几何分布：N＝50，n＝10，不合格品数D＝N×p＝50×0.02=0.5，Ac＝0，则计算接收概率PaPa＝0.9拒收概率为1-Pa＝0.1。

第9题：

某类儿童玩具的不合格率为0. 1，现用抽样方案（10, 1）对多批产品进行抽检，已知每批产品的批量为N = 1000，则：
平均检验总数ATI约为（ ）。
A. 260.8 B. 267.4 C. 280.5 D. 290.6


答案：B
解析：
根据公式ATI =nL(p) + N[ 1 - L(p)] = n + (N - n) [I - L(p)]，代入数据可得，
平均检验总数 ATI = 10 x 0. 74+1000 x(1-0. 74) =267.4。

第10题：

某类儿童玩具的不合格率为0. 1，现用抽样方案（10, 1）对多批产品进行抽检，已知每批产品的批量为N = 1000，则：
平均检出质量AOQ为（ ）。
A. 0. 066 B. 0.074 C. 0.081 D. 0.088


答案：B
解析：
根据公式AOQ≈p(Lp)，代入数据可得，平均检出质量AOQ=0. 1 x 0.74 = 0.074。

更多相关问题
相关内容