军队文职人员招聘
盒内装有10个白球，2个红球，每次取1个球，取后不放回。任取两次，则第二次取得红球的概率是： A. 1/7 B.1/6 C.1/5 D. 1/3
题目
盒内装有10个白球，2个红球，每次取1个球，取后不放回。任取两次，则第二次取得红球的概率是：
A. 1/7
B.1/6
C.1/5
D. 1/3
B.1/6
C.1/5
D. 1/3
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
一个袋内装有10个球，其中有3个白球，5个红球，2个黑球采取不放回抽样，每次取1件，则第二次取到的是白球的概率是()
A、0.6
B、0.5
C、0.4
D、0.3
参考答案：D
第2题：
一个口袋内有4个不同的红球，6个不同的白球.
(1)从中任取4个球，红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?
(1)从中任取4个球，红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?
答案：
解析：
解：(1)由题意知本题是一个分类计数问题.将取出4个球分成三类情况：取4个红
第3题：
袋中有5个球,3个新2个旧,每次取一个,无放回地取两次,则第二次取到新球的概率是()
A、3/5
B、3/4
C、1/2
D、3/10
参考答案：B
第4题：
袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X、Y、Z分别表示两次取球所取得的红、黑与白球的个数。①求
②求二维随机变量(X,Y)的概率分布。
②求二维随机变量(X,Y)的概率分布。答案：
解析：
第5题：
设口袋中有10只红球和15只白球,每次取一个球,取后不放回,则第二次取得红球的概率为_______.
答案：
解析：
设A1={第一次取红球)，A2={第一次取白球），B={第二次取红球），
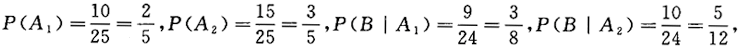
则
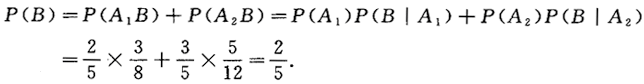
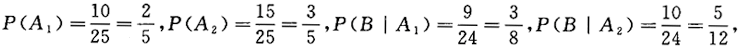
则
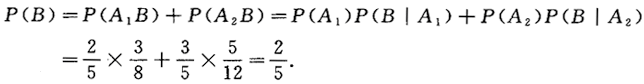
第6题：
盒内装有10个白球，2个红球，每次取1个球，取后不放回。任取两次，则第二次取得红球的概率是：
A. 1/7
B.1/6
C.1/5
D. 1/3
B.1/6
C.1/5
D. 1/3
答案：B
解析：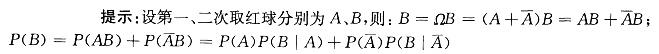
或“试验分两步，求第二步结果的概率”用全概率公式。
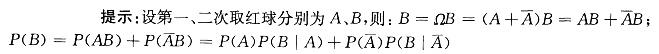
或“试验分两步，求第二步结果的概率”用全概率公式。
第7题：
一个盒子中5个红球,5个白球,现按照如下方式,求取到2个红球和2个白球的概率.
(1)一次性抽取4个球；(2)逐个抽取,取后无放回；(3)逐个抽取,取后放回.
(1)一次性抽取4个球；(2)逐个抽取,取后无放回；(3)逐个抽取,取后放回.
答案：
解析：
【解】(1)设A1={一次性抽取4个球，其中2个红球2个白球），则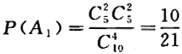
(2)设A2={逐个抽取4个球，取后不放回，其中2个红球2个白球}，则
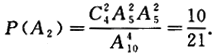
(3)设A3={逐个抽取4个球，取后放回，其中2个红球2个白球}，则
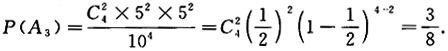
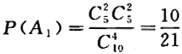
(2)设A2={逐个抽取4个球，取后不放回，其中2个红球2个白球}，则
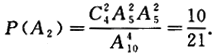
(3)设A3={逐个抽取4个球，取后放回，其中2个红球2个白球}，则
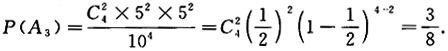
第8题：
一口袋装有6只球，其中4只白球、2只红球。从袋中取球两次，每次随机地取一只。采用不放回抽样的方式，取到的两只球中至少有一只是白球的概率()
A、4/9
B、1/15
C、14/15
D、5/9
参考答案：C
第9题：
从装有4个红球，4个白球的袋中任取4个球，则所取的4个球中包括两种不同颜色的球的概率是：
A33/35
B34/35
C69/70
D7/8
A33/35
B34/35
C69/70
D7/8
答案：B
解析：
第10题：
袋中有1个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球.以X，Y，Z分别表示两次取球所取得的红球、黑球与白球的个数.
(Ⅰ)求P{X=1｜Z=0}；
(Ⅱ)求二维随机变量(X，Y)的概率分布.
(Ⅰ)求P{X=1｜Z=0}；
(Ⅱ)求二维随机变量(X，Y)的概率分布.
答案：
解析：