军队文职人员招聘
设f(x)=dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的().A.等价无穷小 B.同阶但非等价无穷小 C.高阶无穷小 D.低阶无穷小
题目
设f(x)=
dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的().
dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的().
A.等价无穷小
B.同阶但非等价无穷小
C.高阶无穷小
D.低阶无穷小
B.同阶但非等价无穷小
C.高阶无穷小
D.低阶无穷小
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设f(x),g(x),h(x)均为奇函数,则()中所给定的函数是偶函数。
A、f(x)g(x)h(x)
B、[f(x)+g(x)]h(x)
C、f(x)+g(x)
D、f(x)+g(x)+h(x)
参考答案：B
第2题：
设函数f(x)为奇函数,g(x)为偶函数,则复合函数()是奇函数。
A.f(f(x))
B.g(f(x))
C.f(g(x))
D.g(g(x))
正确答案：A
第3题：
设函数f(x)=lnx，g(x)=e2x+1，则f[g(x)]=______。
正确答案：
2x+1
2x+1
第4题：
设f(x)=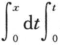
du,g(x)=
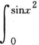（1-cost）dt,则当x→0时,f(x)是g(x)的()
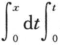du,g(x)=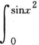（1-cost）dt,则当x→0时,f(x)是g(x)的()A.低阶无穷小
B.高阶无穷小
C.等价无穷小
D.同阶但非等价的无穷小
B.高阶无穷小
C.等价无穷小
D.同阶但非等价的无穷小
答案：A
解析：
第5题：
设f(x)，g(x)ϵP[x J. 若f(x)lg(x)，g(x)lf(x)，则 f(x)与g(x)的关系是( ).
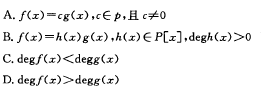
参考答案：A
第6题：
设f (x)=x2,g(x)=ex,则f [g(x)]=_________.
正确答案：
e2x
e2x
第7题：
设f(0)=g(0),且当x30时,f'(x)>g'(x),则当x>0时有()。
A.f(x) B.f(x)>g(x) C.f(x)=g(x) D.以上都不对
正确答案：B
第8题：
设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.
正确答案：
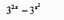
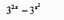
第9题：
设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（ ）。
A． f[g（x）]
B． f[f（x）]
C． g[f（x）]
D． g[g（x）]
B． f[f（x）]
C． g[f（x）]
D． g[g（x）]
答案：D
解析：
D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。
第10题：
设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（ ）。
A． [f（x）/g（x）]＞[f（a）/g（b）]
B． [f（x）/g（x）]＞[f（b）/g（b）]
C． f（x）g（x）＞f（a）g（a）
D． f（x）g（x）＞f（b）g（b）
B． [f（x）/g（x）]＞[f（b）/g（b）]
C． f（x）g（x）＞f（a）g（a）
D． f（x）g（x）＞f（b）g（b）
答案：C
解析：
因为[f（x）g（x）]′＝f′（x）g（x）＋f（x）g′（x）＞0，所以函数f（x）g（x）在[a，b]上单调递增。所以，当x∈（a，b）时，f（a）g（a）＜f（x）g（x）＜f（b）g（b）。