设3阶矩阵A=[α1,α2,α3]有3个不同的特征值,且a3=a1+2a2.(Ⅰ)证明r(A)=2;(Ⅱ)若β=α1,α2,α3,求方程组Ax=β的通解.
题目
设3阶矩阵A=[α1,α2,α3]有3个不同的特征值,且a3=a1+2a2.
(Ⅰ)证明r(A)=2;
(Ⅱ)若β=α1,α2,α3,求方程组Ax=β的通解.
(Ⅰ)证明r(A)=2;
(Ⅱ)若β=α1,α2,α3,求方程组Ax=β的通解.
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设A是n阶矩阵,且E+3A不可逆,则()。
A.3是A的特征值
B.-3是A的特征值
C.1/3是A的特征值
D.-1/3是A的特征值
答案:D
解析:E+3A不可逆,即∣E+3A∣=0,即-3 * ∣(-1/3)E-A∣=0,所以A的特征值为-1/3。
第2题:
设4阶矩阵A与B仅有第3行不同,且|A|=1,|B|=2,则|A+B|=( )。
A.3
B.6
C.12
D.24
B.6
C.12
D.24
答案:D
解析:

第3题:
设三阶矩阵A的特征值为1,1,2,则2A+E的特征值为()。
A、3,5
B、1,2
C、1,1,2
D、3,3,5
参考答案:D
第4题:
设A,B均为4阶矩阵,且|A|=3,|B|=-2,则|-(A'B-1)2|的值为( )。
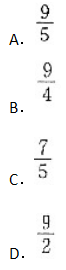
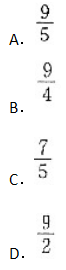
答案:B
解析:
第5题:
设A是3阶矩阵,P=(a1,a2,a3)是3阶可逆矩阵,
若矩阵Q=(a1,a2,a3),则Q-1AQ=


若矩阵Q=(a1,a2,a3),则Q-1AQ=

答案:B
解析:
提示:当P-1AP=Λ时,P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系,a1对应λ1,a2对应λ2,a3对应λ3,可知a1对应特征值λ1=1,a2对应特征值λ2=2,a3对应特征值λ3=0,由此可


第6题:
设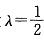 是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
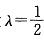 是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
A.3
B.4
C.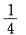
D.1
B.4
C.
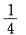
D.1
答案:B
解析:
提示:利用矩阵的特征值与矩阵的关系的重要结论:设λ为A的特征值,则矩阵
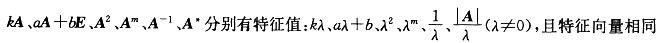

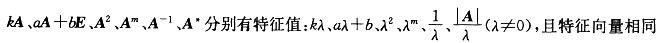

第7题:
设A,B为三阶矩阵,且特征值均为-2,1,1,以下命题:
(1)A~B;(2)A,B合同;(3)A,B等价;(4)|A|=|B|中正确的命题个数为().
(1)A~B;(2)A,B合同;(3)A,B等价;(4)|A|=|B|中正确的命题个数为().
A.1个
B.2个
C.3个
D.4个
B.2个
C.3个
D.4个
答案:B
解析:
因为A,B的特征值为-2,1,1,所以|A|=|B|=-2,又因为r(A)=r(B)=3,所以A,B等价,但A,B不一定相似或合同,选(B).
第8题:
设n阶矩阵A有一个特征值3,则|-3E+A|=_________.
正确答案:
0
0
第9题:
设λ=1/2是非奇异矩阵A的特征值,则矩阵(2A3)-1有一个特征值为:
A. 3 B.4 C.1/4 D. 1
A. 3 B.4 C.1/4 D. 1
答案:B
解析:
提示:利用矩阵的特征值与矩阵的关系的重要结论:设λ为A的特征值,则矩阵kA、aA +bE、A2、Am、A-1 、A*分别有特征值:kλ、aλ+b、λ2、λm、1/λ、 A /λ,且特征向量相同(其中a,b为不等于0的常数,m为正整数)。
矩阵(2A3)-1对应的特征值应是矩阵2A3对应特征值的倒数,下面求矩阵2A3对应的特征值。已知λ=1/2是非奇异矩阵A的特征值,矩阵A3对应的特征值为矩阵A对应的特征值λ=1/2的三次方(1/2)3 ,矩阵2A3对应的特征值为2(1/2)3 =1/4,从而(2A3)-1对应的特征值为1/(1/4)=4。
矩阵(2A3)-1对应的特征值应是矩阵2A3对应特征值的倒数,下面求矩阵2A3对应的特征值。已知λ=1/2是非奇异矩阵A的特征值,矩阵A3对应的特征值为矩阵A对应的特征值λ=1/2的三次方(1/2)3 ,矩阵2A3对应的特征值为2(1/2)3 =1/4,从而(2A3)-1对应的特征值为1/(1/4)=4。
第10题:
设A是三阶矩阵,a1(1,0,1)T,a2(1,1,0)T是A的属于特征值1的特征向量,a3(0,1,2)T是A的属于特征值-1的特征向量,则:
A.a1-a2是A的属于特征值1的特征向量
B.a1-a3是A的属于特征值1的特征向量
C.a1-a3是A的属于特征值2的特征向量
D. a1+a2+a3是A的属于特征值1的特征向量
A.a1-a2是A的属于特征值1的特征向量
B.a1-a3是A的属于特征值1的特征向量
C.a1-a3是A的属于特征值2的特征向量
D. a1+a2+a3是A的属于特征值1的特征向量
答案:A
解析:
提示:已知a1,a2是矩阵A属于特征值1的特征向量,即有Aa1=1*a1,Aa2=1*a2成立,则A(a1-a2)=1*(a1-a2),a1-a2为非零向量,因此a1-a2是A属于特征值1的特征向量。
