甲盒内有红球4只,黑球2只,白球2只;乙盒内有红球5只,黑球3只;丙盒内有黑球2只,白球2只,从这三只盒子的任意一只中任取出一只球,它是红球的概率是( )A.0.5625 B.0.5 C.0.45 D.O.375 E.0.225
题目
甲盒内有红球4只,黑球2只,白球2只;乙盒内有红球5只,黑球3只;丙盒内有黑球2只,白球2只,从这三只盒子的任意一只中任取出一只球,它是红球的概率是( )
A.0.5625
B.0.5
C.0.45
D.O.375
E.0.225
B.0.5
C.0.45
D.O.375
E.0.225
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
某袋内有70个球,其中20个是红球,20个是绿球,20个是黄球,其余是黑球和白球。为确保取出的球中至少包含有10个同色的球,问最少必须从中取出几个球?( )
A. 28
B. 38
C. 18
D. 52
B. 38
C. 18
D. 52
答案:B
解析:
根据题意,黑球和白球个数之和是(70-20X3) = 10(个)。所以同色的10个球只能是红色、绿色或黄色中的一种。假设袋子中只有红球、绿球和黄球三种球,把这三种颜色看做三只抽屉,每只抽屉中放9个球,就要取出9X3 = 27(个)球,如果再多取一个球,就能保证至少有一只抽屉内有10个球,也就是至少有10个同色的球。因为袋中还有10个黑球和白球,取出球的个数只要再加10个,才能保证含有10个同色球。
9X3 +1+ (70-20X3) = 27 + 1 + 10 = 38(个)
最少必须从袋子中取出38个球。故本题选B。
9X3 +1+ (70-20X3) = 27 + 1 + 10 = 38(个)
最少必须从袋子中取出38个球。故本题选B。
第2题:
现有三个箱子,第一个箱子有4个红球,3个白球;第二个箱子有3个红球,3个白球;第三个箱子有3个红球,5个白球;先取一只箱子,再从中取一只球,(1)求取到白球的概率;(2)若取到红球,求红球是从第二个箱子中取出的概率.
答案:
解析:

第3题:
三个箱子,第一个箱子中有4个黑球2个白球,第二个箱子中有3个黑球5个白球,第三个箱子中有3个黑球2个白球。试求:随机地取一个箱子,再从这个箱子中任取出一球,这个球为白球的概率是多少?
参考答案: 

第4题:
一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球,得到黑球 的概率是2/5,从袋中任意摸两个球,至少有一个是白球的概率是7/9,问袋子里有多少个红球?
a.l b.2 c.3 d.4
a.l b.2 c.3 d.4
答案:A
解析: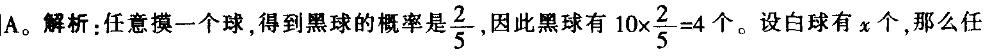
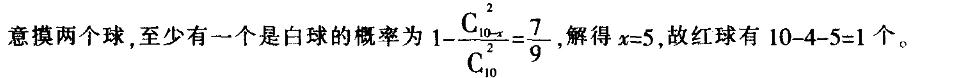
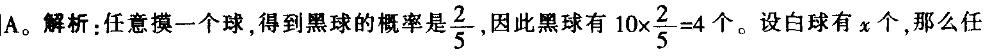
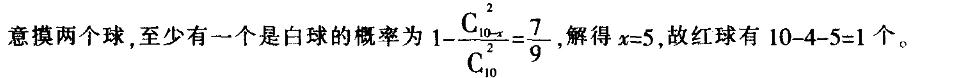
第5题:
甲袋内有2个白球3个黑球,乙袋内有3个白球1个黑球,现从两个袋内各摸出1个球,摸出的两个球都是白球的概率是( )


答案:C
解析:
【考情点拨】本题主要考查的知识点为相互独立事件同时发生的概率. 【应试指导】由已知条件可知此题属于相互独立同时发生的事件,从甲袋内摸到白球的概率


第6题:
现有 A、B 两个容器,容器 A 中有 7 个红球 3 个白球,容器 B 中有 1 个红球 9 个白球,现已 知从这两个容器里任意取出一球,且是红球,则该红球来自容器 A 的概率是:
A.35%
B.50%
C.72.5%
D.87.5%
B.50%
C.72.5%
D.87.5%
答案:D
解析:
两个容器共有8个红球,任取一个球是红球有8种情况,其中有7种情况来自容器A,则红球来自容器A的概率是7÷8=87.5%。
第7题:
有三个盒子,第一个盒子有4个红球1个黑球,第二个盒子有3个红球2个黑球,第三个盒子有2个红球3个黑球,如果任取一个盒子,从中任取3个球,以X表示红球个数.
(1)写出X的分布律;(2)求所取到的红球数不少于2个的概率.
(1)写出X的分布律;(2)求所取到的红球数不少于2个的概率.
答案:
解析: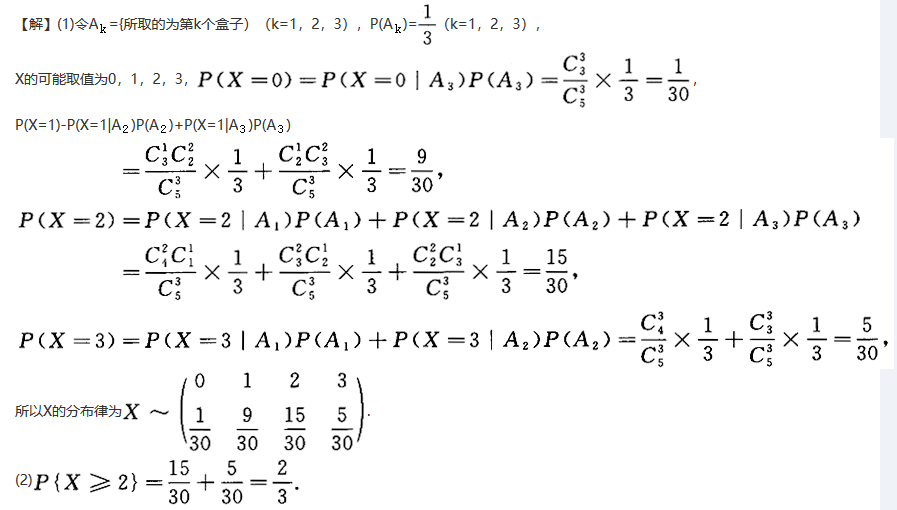
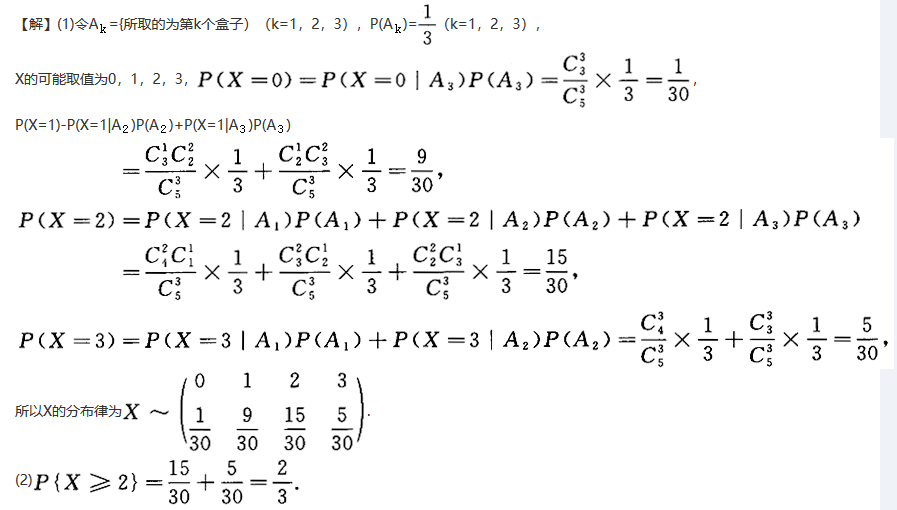
第8题:
甲袋有白球3只,红球7只,黑球l5只。乙袋有白球10只,红球6只,黑球9只。现从两袋中各取一个,试求两球颜色相同的概率约为( )。
A.0.17
B.0.33
C.0.45
D.0.8
正确答案:B


第9题:
将2个红球与1个白球随机地放入甲、乙、丙三个盒子中,则乙盒中至少有1个红球的概率为
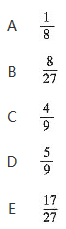
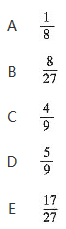
答案:D
解析: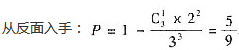
第10题:
一布袋中有红球8个,白球5个和黑球12个,它们除颜色外没有其他区别,随机地从袋中取出1球不是黑球的概率为( )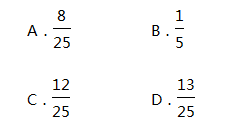
答案:D
解析:
