公共基础

单选题口袋里装有10只外形相同的球，其中7只红球，3只白球．从口袋中任意取出2只球，则它们是一只红球、一只白球的概率等于（）．A 21/90.B 21/45C 21/100D 21/50

题目
单选题
口袋里装有10只外形相同的球，其中7只红球，3只白球．从口袋中任意取出2只球，则它们是一只红球、一只白球的概率等于（）．
A

21/90.

B

21/45

C

21/100

D

21/50

如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案

第1题：

一口袋装有6只球，其中4只白球、2只红球。从袋中取球两次，每次随机地取一只。采用不放回抽样的方式，取到的两只球中至少有一只是白球的概率()

A、4/9

B、1/15

C、14/15

D、5/9


参考答案：C

第2题：

在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球?

A．14

B．15

C．17

D．18


正确答案：B
[答案] B。解析：抽屉原理，最坏的情况是10个黑球和4个红球都拿出来了，第15次拿到的肯定是白球。

第3题：

口袋里有3个红球和2个白球，球除颜色外完全相同，从中任意摸出1个球。那么，摸出红球的可能性是_____，摸出白球的可能性是_____。要使它们的可能性相同，可以怎么做？


3/5；2/5；拿走一个红球

第4题：

一位乒乓球学员手中拿着装有7只乒乓球的不透明口袋,其中3只黄球，4只白球。他随机取出一只乒乓球，观察颜色后放回袋中，同时放入2只与取出的球同色的球，这样连续取2次，则他取出的两只球中第1次取出的是白球，第2次取出的是黄球的概率是

A.8/77
B.4/21
C.2/11
D.4/7

答案：B
解析：
第一步，第一次取出白球的概率为4/7。第二步，由题意取出白球后会再放入2个白球，球的总数为9。第二次取出黄球的概率为3/9=1/3，故第一次取出白球，第二次取出黄球的概率为4/7×1/3=4/21。因此，选择B选项。

第5题：

袋中有5个大小相同的球，其中3个是白球，2个是红球，一次随机地取出3个球，其中恰有2个是白球的概率是：


答案：D
解析：

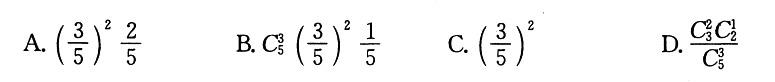
第6题：

（3）一个口袋内装有除颜色外其他都相同的6个白球和4个红球，从中任意摸出2个，求：A、2个都是白球的概率；B、2个都是红球的概率；C、一个白球，一个红球的概率。


正确答案：
          

第7题：

箱子里有红、白两种玻璃球。红球是向球的3倍少2个。每次从箱子里取出7个白球、13个红球，经过若干次后，箱子里剩下6个白球，72个红球，那么，原来箱子里红球比白球多多少个?（ ）

A．102

B．104

C．106

D．108


正确答案：D
假设箱子里原来有白球x个，那么红球为(3x--2)个，依题意有(x－6)÷7=(3x－2－72)÷13，解得x=55，所以原来红球比白球多3×55－2－55=108(个)。故选D。

第8题：

在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球？

A．14 B．15 C．17 D．18


正确答案：B

抽屉原理，最坏的情况是10个黑球和4个白球都拿出来了，最后第15次拿到的肯定是白球。

第9题：

现有 A、B 两个容器，容器 A 中有 7 个红球 3 个白球，容器 B 中有 1 个红球 9 个白球，现已 知从这两个容器里任意取出一球，且是红球，则该红球来自容器 A 的概率是：

A.35%
B.50%
C.72.5%
D.87.5%

答案：D
解析：
两个容器共有8个红球，任取一个球是红球有8种情况，其中有7种情况来自容器A，则红球来自容器A的概率是7÷8=87.5%。

第10题：

现有三个箱子,第一个箱子有4个红球,3个白球；第二个箱子有3个红球,3个白球；第三个箱子有3个红球,5个白球；先取一只箱子,再从中取一只球,(1)求取到白球的概率；(2)若取到红球,求红球是从第二个箱子中取出的概率.


答案：
解析：

更多相关问题
相关内容