自学考试专题:自考04184线性代数(经管类)自考核心考点笔记
A.有相同的特征值
B.有相同的特征向量
C.有两两正交的特征向量
A.实对称阵
B.有n个相异特征值的n阶阵
C.有n个线性无关的特征向量的n阶方阵
A.A的n个特征向量两两正交
B.A的n个特征向量组成单位正交向量组
C.A的k重特征值λ0,有r(λ0E-A)=n-k
D.A的k重特征值λ。,有r(λ0E-A)=k

n*n矩阵可看作是n维空间中的线性变换,矩阵的特征向量经过线性变换后,只是乘以某个常数(特征值),因此,特征向量和特征值在应用中具有重要的作用。下面的矩阵(其中w1、w2、w3均为正整数)有特征向量(w1,w2,w3),其对应的特征值为( )。

A.1/3
B.1
C.3
D.9
解析:n*n矩阵可看做是n维空间中的线性变换,它将任何一个向量x变换成新的向量(A的矩阵与列向量x的乘积)。三维空间中的旋转变换就是一种线性变换,它将一个变量变换成另一个变量。旋转变换必然绕某个轴旋转,这个轴上的向量经过该旋转变换后得到的向量仍会保持在这根轴上。这根轴上的向量属于该旋转变换的特征向量。对于单纯的旋转变换来说,这根旋转轴上的特征向量所对应的特征值为1。线性变换A的特征向量Y及其相应的特征值λ满足AY=λY,其几何意义是特征向量Y经过线性变换A变换成向量λY(保持在同一轴上,只是乘以常数λ,放大或缩小入倍,λ为负时变为相反方向)。本题中的矩阵A以及由w1、w2、w3组成的列向量w具有关系(可以通过矩阵乘法得到)Aw=3w,所以,(w1、w2、w3)是该矩阵的特征向量,其相应的特征值为3。

>>a=[2,4,9;4,2,4;9,4,18]
>>eig(a)
A.ns=-3.0645
1.7042
23.3603
第一章 行列式 1.1 行列式的定义 1.2 行列式行(列)展开 1.3 行列式的性质与计算 1.3 克拉默法则 第二章 矩阵 2.1 线性方程组与矩阵的定义 2.2 矩阵运算 2.3 分阵的逆矩阵 2.4 分块矩阵 2.5 矩阵的初等变换与初等方阵 2.6 矩阵的秩 2.7 矩阵与线性方程组 第三章 向量空间 3.1 n维向量概念及其线性运算 3.2 线性相关与线性无关 3.3 向量组的秩 3.4 向量空间 第四章 线性方程组 4.1 齐次线性方程组 4.2 非齐次线性方程组 第五章 特征值与特征向量 5.1 特征值与特征向量 5.2 方阵的相似变换 5.3 向量内积和正交矩阵 5.4 实对称矩阵的相似标准形 第六章 实二次型 6.1 实二次型及其标准形 6.2 正这二次型和正定矩阵 (中间部分略) 完整版15页请QQ:1273114568 索取第一部分行列式本章概述 行列式在线性代数的考试中占很大的比例。从考试大纲来看。虽然只占13%左右。但在其他章。的试题中都有必须用到行列式计算的内容。故这部分试题在试卷中所占比例远大于13%。1.1行列式的定义1.1.1二阶行列式与三阶行列式的定义一、二元一次方程组和二阶行列式例1.求二元一次方程组的解。解:应用消元法得当时。得同理得定义 称为二阶行列式。称为二阶行列式的值。记为。于是 由此可知。若。则二元一次方程组的解可表示为:例2二阶行列式的结果是一个数。我们称它为该二阶行列式的值。二、三元一次方程组和三阶行列式考虑三元一次方程组希望适当选择。使得当后将消去。得一元一次方程若,能解出其中要满足为解出。在(6),(7)的两边都除以得这是以为未知数的二元一次方程组。 定义1.1.1 在三阶行列式中,称于是原方程组的解为;类似地得 这就将二元一次方程组解的公式推广到了三元一次方程组。例3 计算例4 (1)(2)例5 当x取何值时,?为将此结果推广到n元一次方程组。需先将二阶、三阶行列式推广到n阶行列式。1.1.2阶行列式的定义定义1.1.2 当n时,一阶行列式就是一个数。当时,称为n阶行列式。定义(其所在的位置可记为的余子式的代数余子式。定义 为该n阶行列式的值。即。容易看出,第j列元素的余子式和代数余子式都与第j列元素无关;类似地,第i行元素的余子式和代数余子式都与第i行元素无关。n阶行列式为一个数。例6 求出行列式第三列各元素的代数余子式。例7 (上三角行列式)1.2行列式按行(列)展开定理1.2.1(行列式按行(列)展开定理)例1 下三角行列式主对角线元素的乘积。例2 计算行列式例3 求n阶行列式小结 1.行列式中元素的余子式和代数余子式的定义。2.二阶行列式的定义。3.阶行列式的定义。即。4.行列式按行(列)展开的定理和应用这个定理将行列式降阶的方法。1.3行列式的性质及计算1.3.1行列式的性质给定行列式将它的行列互换所得的新行列式称为D的转置行列式,记为或。性质1 转置的行列式与原行列式相等。即性质2 用数k乘行列式D的某一行(列)的每个元素所得的新行列式等于kD。推论1 若行列式中某一行(列)的元素有公因数,则可将公因数提到行列式之外。推论2 若行列式中某一行(列)的元素全为零,则行列式的值为0。 (中间部分略) 完整版15页请QQ:1273114568 索取性质3 行列式的两行(列)互换,行列式的值改变符号。以二阶为例设推论3 若行列式某两行(列),完全相同,则行列式的值为零。证 设中,第i行与第j行元素完全相同,则所以,D=0。性质4 若行列式某两行(列)的对应元素成比例,则行列式的值为零。性质5 若行列式中某一行(列)元素可分解为两个元素的和,则行列式可分解为两个行列式的和,即只要看注意 性质中是指某一行(列)而不是每一行。可见性质6 把行列式的某一行(列)的每个元素都乘以 加到另一行(列),所得的行列式的值不变。证.1.3.2行列式的计算人们认识事物的基本方法是化未知为已知。对行列式,先看何为已知,(1)二,三阶行列式的计算;(2)三角形行列式的计算。因此,我们计算行列式的基本方法是利用行列式的性质把行列式化为三角形,或降阶。例1 计算在行列式计算中如何造零是个重要技巧,主要是应用性质6。例2 计算例3 计算例4 计算例5 计算扩展计算例6 计算方法1方法2扩展:计算例7 计算例8 计算扩展:计算例9 计算n阶行列式 解 按第一列展开,得例10 范德蒙行列式.例11 计算例12 证明小结1.准确叙述行列式的性质;2.应用行列式的性质计算行列式的方法(1)低阶的数字行列式和简单的文字行列式;(2)各行元素之和为相同的值的情况(3)有一行(列)只有一个或两个非零元的情况1.4克拉默法则这一节将把二元一次方程组解的公式推广到n个未知数,n个方程的线性方程组。为此先介绍下面的定理。定理1.4.1 对于n阶行列式证 由定理1.2.1知 ,注意改变第二列的元素,并不改变第二列元素的代数余子式类似地,可证明该定理的剩余部分。定理1.4.2 如果n个未知数,n个方程的线性方程组 的系数行列式 则方程组有惟一的解: 其中 证明从略例1.求解把克拉默法则应用到下面的齐次方程组有定理1.4.3 如果n个未知数n个方程的齐次方程组的系数行列式D0,则该方程组只有零解,没有非零解。推论如果齐次方程组有非零解,则必有系数行列式D=0。事实上,以后我们将证明对于由n个未知数n个方程的齐次方程组,系数行列式D=0,不仅是该齐次方程组有非零解的必要条件,也是充分条件,即若系数行列式D=0,则齐次方程组必有非零解。例2判断线性方程组 (中间部分略) 完整版15页请QQ:1273114568 索取是否只有零解例3当k为何值时,齐次方程组没有非零解?例4问当 取何值时,齐次方程组有非零解?1.定理1.4.1 对于,有2.n个未知数,n个方程的线性方程组的克拉默法则。以及n个未知数, n个方程的齐次线性方程组有非零解的充分必要条件。第一章小结基本概念1.行列式中元素的余子式和代数余子式。2.行列式的定义基本公式1.行列式按一行(一列)展开的定理;2.行列式的性质;3.行列式中任一行(列)与另一行(列)的代数余子式乘积的和=0;4.克拉默法则5.n个未知数,n个方程的齐次方程组有非零解的充分必要条件是它的系数行列式=0。重点练习内容1.行列式中元素的余子式和代数余子式的计算;2.行列式的计算及重点例题(1)二、三阶行列式的计算;方法:利用行列式的性质降阶。(2)各行元素之和为常数的情况(重点例题:1.3节中例5及其扩展);(3)特殊的高阶行列式。所以例7 矩阵必不正定。 6.2.3二次型的分类定义6.2.3 设Ax是n元二次型,其中A是实对称矩阵。二次型可分成以下五类:(1)如果对于任意的非零实列向量x,都有,则称该二次型正定,称此二次型的矩阵A为正定矩阵。(2)如果对于任意的实列向量x,都有,则称该二次型半正定,称此二次型的矩阵A为半正定矩阵。(3)如果对于任意的非零实列向量x,都有 ,则称该二次型负定,称此二次型的矩阵A为负定矩阵
对应特征向量为(-1,0,1)^T.
(1)求A的其他特征值与特征向量;
(2)求A.

 (b>0),
(b>0),
其中二次型的矩阵A的特征值之和为1,特征值之积为-12.
(1)求a,b的值;
(2)利用正交变换将二次型f化为标准形,并写出所用的正交变换和对应的正交矩阵.


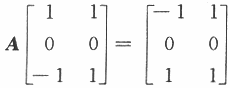
(Ⅰ)求A的所有特征值与特征向量;
(Ⅱ)求矩阵A.


在正交变换下的标准方程的图形如图所示,

则A的正特征值的个数为
B.1
C.2
D.3
 =1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
=1其次,二次型经正交变换化为标准形时,其平方项的系数就是A的特征值,所以应选(B).
很多考生选择(C),是不是把标准方程记成了图1} 而忽略了本题的条件是x^TAx=1.
