一平面谐波以u的速率沿x轴正向传播,角频率为w。那么,距原点x处(x>0)质点的振动相位与原点处质点的振动相位相比,有下列哪种关系?()A、滞后wx/uB、滞后x/uC、超前wx/uD、超前x/u
题目
一平面谐波以u的速率沿x轴正向传播,角频率为w。那么,距原点x处(x>0)质点的振动相位与原点处质点的振动相位相比,有下列哪种关系?()
- A、滞后wx/u
- B、滞后x/u
- C、超前wx/u
- D、超前x/u
如果没有搜索结果,请直接 联系老师 获取答案。
如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
一平面简谐波沿x轴正向传播,已知P点(xp=L)的振动方程为y=Acos(ωt+φ0),则波动方程为( )。
A.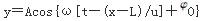
B.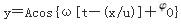
C.y=Acos[t-(x/u)]
D.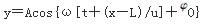
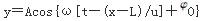
B.
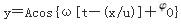
C.y=Acos[t-(x/u)]
D.
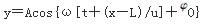
答案:A
解析:
振动由P点传到x点所需时间为(x-L)/u,即P点的位相比x点的位相落后了ω(x-L)/u。
第2题:
一简谐波沿x轴正向传播,波的振幅为A,角频率为ω,波速为u。若以原点处的质元经平衡位置正方向运动时作为计时的起点,则该波的波动方程是( )。
A.y=Acos[ω(t-x/u)+π/2]
B.y=Acos[ω(t-x/u)-π/2]
C.y=Acos[ω(t-x/u)+π]
D.y=Acos[ω(t-x/u)-π/3]
B.y=Acos[ω(t-x/u)-π/2]
C.y=Acos[ω(t-x/u)+π]
D.y=Acos[ω(t-x/u)-π/3]
答案:B
解析:
第3题:
一平面简谐波在t=0时的波形曲线如图所示,设波沿x轴正向传播,波速υ=1.6×10-1m/s,则该波的角频率ω=______rad/s,坐标原点处的质元作简谐振动的表达式为y=_____(SI)。
正确答案:
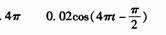
第4题:
一平面简谐波沿x轴正向传播,已知波长λ,频率v,角频率w,周期T,初相Φ0,则下列表示波动方程的式子中,哪几个是正确的?
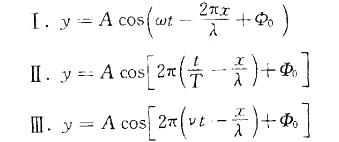
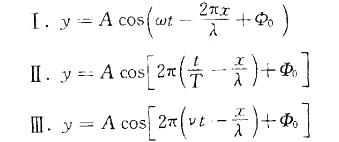
A.Ⅰ
B.Ⅰ、Ⅱ
C.Ⅱ、Ⅲ
D.Ⅰ、Ⅱ、Ⅲ
B.Ⅰ、Ⅱ
C.Ⅱ、Ⅲ
D.Ⅰ、Ⅱ、Ⅲ
答案:D
解析:
提示:μ=λv,w=2πv。
第5题:
一平面谐波以u的速率沿x轴正向传播,角频率为ω,那么,距原点x处(x>0)质点的振动相位与原点处质点的振动相位相比,具有的关系是( )。
A.滞后ωx/u
B.滞后x/u
C.超前ωx/u
D.超前x/u
B.滞后x/u
C.超前ωx/u
D.超前x/u
答案:A
解析:

第6题:
一平面简谐波沿X轴正向传播,已知x=L(L<λ)处质点的振动方程为y=Acosωt,波速为u,那么x=0处质点的振动方程为( )。
A.y=Acosω(t+L/u)
B.y=Acosω(t-L/u)
C.y=Acos(ωt+L/u)
D.y=Acos(ωt-L/u)
B.y=Acosω(t-L/u)
C.y=Acos(ωt+L/u)
D.y=Acos(ωt-L/u)
答案:A
解析:
以x=L处为原点,写出波动方程,再令x=-L代入波动方程。
第7题:
一平面简谐波沿X轴正向传播,已知x=L(L0),波速为u,那么x=0处质点的振动方程为:
A. y=Acos[w(t+l/u)+Φ0]
B.y=Acos[w(t-l/u)+Φ0]
C. y=Acos[wt+l/u+Φ0]
D. y=Acos[wt-l/u+Φ0]
B.y=Acos[w(t-l/u)+Φ0]
C. y=Acos[wt+l/u+Φ0]
D. y=Acos[wt-l/u+Φ0]
答案:A
解析:
提示:以x=L处为原点,写出波动方程,再令x=-L。
第8题:
一列沿x轴正向传播的平面简谐波,波长为4m。当波源的零相位传播到x=0处时,波源的π相位正好传播到的位置为( )
A.x=-2m
B.x=0
C.x=2m
D.x=4m
正确答案:C
第9题:
一平面谐波以u的速率沿x轴正向传播,角频率为w。那么,距原点x处(x>0) 质点的振动相位与原点处质点的振动相位相比,有下列哪种关系?
B.滞后wx/u D.超前x/u
A.滞前wx/u Ct 超前x/u
B.滞后wx/u D.超前x/u
A.滞前wx/u Ct 超前x/u
答案:A
解析:
提示:复习机械波(行波)的发生。
第10题:
一平面谐波以速度u沿x轴正向传播,角频率为ω,那么距原点X处(X>0) 质点的振动相位与原点处的振动相位相比,有下列哪种关系?( )
A.滞后ωX/uB.滞后X/u C.超前ωX/u D.超前X/u
A.滞后ωX/uB.滞后X/u C.超前ωX/u D.超前X/u
答案:A
解析:
