下列属于认识平面图形教育的指导要点的是（）。A、感知图形的基本特征B、通过比较来掌握新的图形特征及名称C、加深和巩固对图形的认识D、突出重难点

(1)课题引入：(引导性材料)
想一想：怎样的两个图形叫做关于某直线成轴对称 成轴对称的两个图形有什么特点
(帮助学生复习轴对称的有关知识，为中心对称教学作准备)
画一画：如图l(1)，已知点P和直线l，画出点P关于直线，的对称点P，；如图l(2)，已知线段MN和直线
a．画出线段MN关于直线a的对称线段M’N’。
(通过画图形进一步巩固和加深对轴对称的认识)
上述问题由学生回答．教师作必要的提示．并归纳总结成下表：

观察与思考：图2所示的图形关于某条直线成轴对称吗 如果是，画出对称轴，如果不是，说明理由。

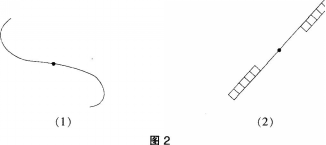
(教师把图2的两个图形制成投影片或教具，学生仔细观察后，能发现这两个图形都不是轴对称。然后，教师适时提出问题：这两个图形能不能重合 怎样才能使这两个图形重合呢 让学生观察、探究、讨论，教师可以直观地演示中心对称变换的过程，让学生发现：把其中一个图形统一特殊点旋转l80度后能与另一个图形重合。)
问题l：你能举出1～2个实例或实物，说明它们也具有上面所说的特性吗
说明：学生自己举例有助于他们感性地认识中心对称的意义。然后，教师指出：具有这种特性的图形叫做中心对称图形，并介绍对称中心，对称点等概念。
问题2：你能给“中心对称”下一个定义吗
说明与建议：学生下定义会有困难，教师应及时修正，并给出明确的定义，然后指出定义中的三个要点：
①有一个对称中心——点；②图形绕中心旋转l80度；③旋转后与另一图形重合。把这三要点填入引导性材料中的空表内，在顶空格内写上“中心对称”字样，以利于写“轴对称”进行比较。
(2)教学环节：
环节l：练一练：在图3中．已知AABC和AEFG关于点0成中心对称，分别找出图中的对称点和对称线段。


说明与建议：教师可演示△ABC绕点0旋转l80度后与△EFG重合的过程，让学生说出点E和点A，点B和点F，点C和点G是对称点；线段AB和EF、线段AC和EG，线段BC和FG都是对称线段。教师还可向学生指出，上图中，点A、0、E在一条直线上，点C、0、G在一条直线上，点8、0、F在一条直线上，且AO=E0，BO=F0，
CO=G0。
问题：从上面的练习及分析中，可以看出关于中心对称的两个图形具有哪些性质
说明与建议：引导学生总结出关于中心对称的两个图形的性质：定理l——关于中心对称的两个图形是全等形；定理2——关于中心对称的两个图形，对称点连线都经过对称中心．并且被对称中心平分。
问题：定理2的题设和结论各是什么 试说出它的逆命题。
说明与建议：学生解答此题有困难，教师要及时引导。特别是叙述命题时，学生常常照搬“对称点”“对称中心”这些词语，教师应指出：由于没有“两个图形关于中心对称”的前提．所以不能使用“对称点”“对称中心”这样的词语，而要改为“对应如”“某一点”。最后，教师应完整地叙述这个逆命题——如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于点对称。
问题：怎样证明这个逆命题是正确的
说明与建议：证明过程应在教师的引导下，师生共同完成。由已知条件——对应点的连线都经过某一点，并且被这一点平分，可以知道：若把其中一个图形绕着这点旋转180度，它必定与另一个图形重合，因此．根据定义可以判定这两个图形关于这一点对称。这个逆命题即为逆定理。根据这个逆定理，可以判定两个图形关于一点对称，也可以画出已知图形关于一点的对称图形。
环节2：练一练：画出图4中，线段PQ关于点D的对称线段PQ’。


(画法如下：(1)连结PD，延长PO到P，使0P'=OP，点P，就是点P关于点0的对称点。(2)连结Q0，延长Q0到Q’，使Q’Q=OQ，点Q’就是点Q的对称点，则PQ’就是线段PQ关于0点的对称线段。教师应指出：画一个图形关于某点的中心对称图形，关键是画“对称点”。比如，画一个三角形关于某点的中心对称三角形，只要画出三角形三个顶点的对称点，就可以画出所要求的三角形。)

幼儿数学教育内容的系统性是指在数学教育内容的选择和安排上，应遵循数学知识的逻辑性和幼儿学习的逻辑顺序，体现先易后难、循序渐进、前后联系的特点。小、中班幼儿以认识平面图形为主，大班幼儿可以学习认识几何体，反映的是数学教育内容的系统性。

(1)课题引入：(引导性材料) 想一想：怎样的两个图形叫作关于某直线成轴对称成轴对称的两个图形有什么特点
(帮助学生复习轴对称的有关知识，为中心对称教学做准备)

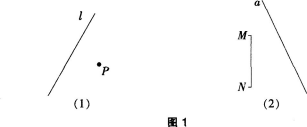
画一画：如图1(1)，已知点P和直线ι，P出点P关于直线Z的对称点P′；如图1(2)，已知线段MN和直线a，匦出线段MN关于直线a的对称线段M′N′。
(通过画图形进一步巩固和加深对轴对称的认识)
上述问题由学生回答，教师作必要的提示，并归纳总结成下表：

观察与思考：图2所示的图形关于某条直线成轴对称吗如果是，画出对称轴；如果不是，说明理由。

(教师把图2的两个图形制成投影片或教具，学生仔细观察后，能发现这两个图形都不是轴对称。然后，教师适时提出问题：这两个图形能不能重合怎样才能使这两个图形重合呢让学生观察、探究、讨论，教师可以直观地演示中心对称变换的过程，让学生发现：把其中一个图形统一特殊点旋转180度后能与另一个图形重合。)
问题1：你能举出1～2个实例或实物．说明它们也具有上面所说的特性吗
说明：学生自己举例有助于他们感性地认识中心对称的意义。然后，教师指出：具有这种特性的图形叫作中心对称图形．并介绍对称中心，对称点等概念。
问题2：你能给“中心对称”下一个定义吗
说明与建议：学生下定义会有困难，教师应及时修正，并给出明确的定义，然后指出定义中的三个要点：
①有一个对称中心——点；②图形绕中心旋转180度；③旋转后与另一图形重合。把这三要点填入引导性材料中的空表内，在顶空格内写上“中心对称”字样，以利于写“轴对称”进行比较。
(2)教学环节：
环节1：练一练：在图3中，已知△ABC和△EFG关于点O成中心对称，分别找出图中的对称点和对称线段。

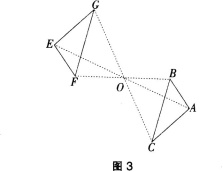
说明与建议：教师可演示△ABC绕点O旋转180度后与△EFG重合的过程，让学生说出点E和点A，点B和点F，点C和点G是对称点；线段AB和EF、线段AC和EG，线段BC和FG都是对称线段。教师还可向学生指出，上图中，点A、O、E在一条直线上，点C、O、G在一条直线上，点B、O、F在一条直线上，且AO=EO，BO=FO，CO=GO。
问题：从上面的练习及分析中，可以看出关于中心对称的两个图形具有哪些性质
说明与建议：引导学生总结出关于中心对称的两个图形的性质：定理1——关于中心对称的两个图形是全等形；定理2——关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
问题：定理2的题设和结论各是什么试说出它的逆命题。
说明与建议：学生解答此题有困难，教师要及时引导。特别是叙述命题时。学生常常照搬“对称点”“对称中心”这些词语，教师应指出：由于没有“两个图形关于中心对称”的前提。所以不能使用“对称点”“对称中心”这样的词语，而要改为“对应如”“某一点”。最后，教师应完整地叙述这个逆命题——如果两个图形的对应点连线都经过某一点，并且被这一点平分。那么这两个图形关于点对称。
问题：怎样证明这个逆命题是正确的
说明与建议：证明过程应在教师的引导下，师生共同完成。由已知条件——对应点的连线都经过某一点，并且被这一点平分，可以知道：若把其中一个图形绕着这点旋转180度，它必定与另一个图形重合，因此，根据定义可以判定这两个图形关于这一点对称。这个逆命题即为逆定理。根据这个逆定理，可以判定两个图形关于一点对称，也可以画出已知图形关于一点的对称图形。
环节2：练一练：画出图4中，线段PQ关于点O的对称线段P′Q′。

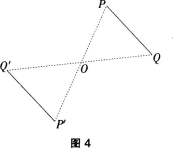
(画法如下：(1)连结PO，延长PO到P′，使OP′=OP，点P，就是点P关于点O的对称点。(2)连结QO，延长QO到Q′，使Q′Q=OQ，点Q′就是点Q的对称点，则PQ′就是线段PQ关于O点的对称线段。教师应指出：画一个
图形关于某点的中心对称图形，关键是画“对称点”。比如，画一个三角形关于某点的中心对称三角形，只要画出三角形三个顶点的对称点，就可以画出所要求的三角形。)