数学
单选题设α1，α2，α3，α4是4维非零列向量组，A=（α1，α2，α3，α4），A*是A的伴随矩阵，已知方程组AX=0的基础解系为k（1，0，2，0）T，则方程组A*X=0的基础解系为（ ）.A α1，α2，α3B α1+α2，α2+α3，3α3C α2，α3，α4D α1+α2，α2+α3，α3+α4，α4+α1
题目
单选题
设α1，α2，α3，α4是4维非零列向量组，A=（α1，α2，α3，α4），A*是A的伴随矩阵，已知方程组AX=0的基础解系为k（1，0，2，0）T，则方程组A*X=0的基础解系为（ ）.
A
α1，α2，α3
B
α1+α2，α2+α3，3α3
C
α2，α3，α4
D
α1+α2，α2+α3，α3+α4，α4+α1
如果没有搜索结果，请直接 联系老师 获取答案。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设A是4×5矩阵，ξ1，ξ2是齐次线性方程组Ax=0的基础解系，则下列结论正确的是( ).
A.ξ1-ξ2，ξ1+2ξ2也是Ax=0的基础解系
B.k1ξ1+k1ξ2是Ax=0的通解
C.k1ξ1+ξ2是Ax=0的通解
D.ξ1-ξ2，ξ2-ξ1也是Ax=0的基础解系
B.k1ξ1+k1ξ2是Ax=0的通解
C.k1ξ1+ξ2是Ax=0的通解
D.ξ1-ξ2，ξ2-ξ1也是Ax=0的基础解系
答案：A
解析：
由题设知道，n=5，s=n-r=2，r=3.B不正确，因为k1ξ1+k1ξ2=k1(ξ2+ξ1)只含有一个不定常数，同样理由说明C也不正确.D不正确，因为(ξ1-ξ2)+(ξ1+ξ2)=0，这表明ξ1-ξ2与ξ2-ξ1线性相关.A正确，因为ξ1-ξ2与ξ1+2ξ2都是Ax=0的解，且它 们线性无关，故选A.
第2题：
设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().
A.矩阵A不可逆
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量
答案：C
解析：
由λ1=-1，λ2=0，λ3=1得|A|=0，则r(A)小于3，即A不可逆，(A)正确；又λ1+λ2+λ3=tr(A)=0，所以(B)正确；因为A的三个特征值都为单值，所以A的非零特征值的个数与矩阵A的秩相等，即r(A)=2，从而AX=0的基础解系仅含有一个线性无关的解向量，(D)是正确的；(C)不对，因为只有实对称矩阵的不同特征值对应的特征向量正交，一般矩阵不一定有此性质，所以选(C).
第3题：
设A是4×6矩阵，r（A）=2，则齐次线性方程组Ax=0的基础解系中所含向量的个数是（ ）
A.1 B.2
C.3 D.4
正确答案：D
第4题：
设A=(α1，α2，α3)为3阶矩阵.若α1，α2线性无关，且α3=-α1+2α1，则线性方程组Ax=0的通解为________.
答案：
解析：
1、k(1，-2，1)^T，k为任意常数
1、k(1，-2，1)^T，k为任意常数
第5题：
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3，且η1，η2，η3是3个不同的解向量，则通解是( ).
A.x=k1(η-η2)+η3
B.x=k1η1+k2η2+η3
C.x=k1η1+k2η2+k3η3
D.x=k1(η+η2)+η3
B.x=k1η1+k2η2+η3
C.x=k1η1+k2η2+k3η3
D.x=k1(η+η2)+η3
答案：A
解析：
由n=4，r=3得s=1。ηη2是 Ax=0的基础解系
第6题：
设有方程组AX=O与BX=0,其中A,B都是m×N阶矩阵,下列四个命题：
(1)若AX=O的解都是BX=O的解,则r(A)≥r(B)
(2)若r(A)≥r(B),则AX=0的解都是BX=0的解
(3)若AX=0与BX=0同解,则r(A)-r(B)
(4)若r(A)=r（B）,则AX=0与BX=0同解
以上命题正确的是().
(1)若AX=O的解都是BX=O的解,则r(A)≥r(B)
(2)若r(A)≥r(B),则AX=0的解都是BX=0的解
(3)若AX=0与BX=0同解,则r(A)-r(B)
(4)若r(A)=r（B）,则AX=0与BX=0同解
以上命题正确的是().
A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(3)(4)
B.(1)(3)
C.(2)(4)
D.(3)(4)
答案：B
解析：
若方程组AX=0的解都是方程组BX=0的解，则n-r(A)≤n-r(B)，从而 r(A)≥r(B)，(1)为正确的命题；显然(2)不正确；因为同解方程组系数矩阵的秩相等，但
反之不对，所以(3)是正确的，(4)是错误的，选(B).
反之不对，所以(3)是正确的，(4)是错误的，选(B).
第7题：
设n阶矩阵A的伴随矩阵A^*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次线性方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系
A.不存在.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.
答案：B
解析：
第8题：
对于有5个变量的齐次线性方程组AX=0,系数矩阵的秩r(A)=3,则其基础解析中向量个数为()。
A.2
B.5
C.3
D.1
正确答案：A
第9题：
设3阶实对称矩阵A的各行元素之和都为3,向量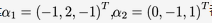
都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵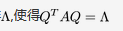
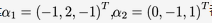都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵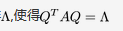答案：
解析：
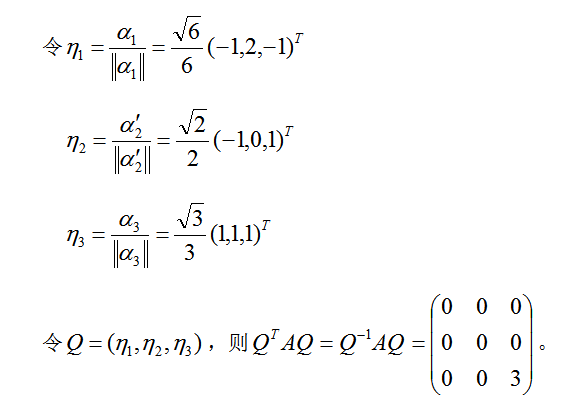
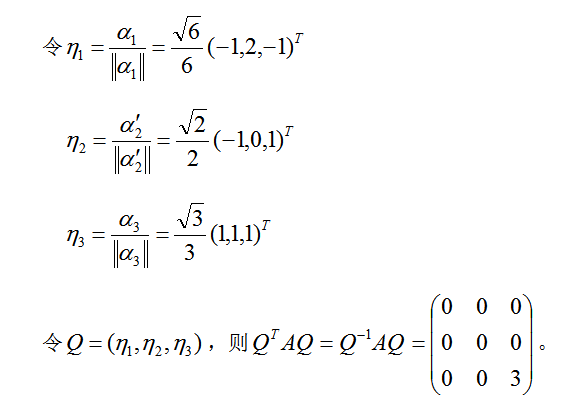
第10题：
设3阶矩阵A=［α1，α2，α3］有3个不同的特征值，且a3=a1+2a2.
(Ⅰ)证明r(A)=2；
(Ⅱ)若β=α1，α2，α3，求方程组Ax=β的通解.
(Ⅰ)证明r(A)=2；
(Ⅱ)若β=α1，α2，α3，求方程组Ax=β的通解.
答案：
解析：