专业科目
单选题已知函数yt＝t（t－1）/2＋C是方程yt＋1－yt＝f（t）的解，则f（t）＝（ ）。A t－1B t－2C tD 2－t
题目
单选题
已知函数yt＝t（t－1）/2＋C是方程yt＋1－yt＝f（t）的解，则f（t）＝（ ）。
A
t－1
B
t－2
C
t
D
2－t
参考答案和解析
正确答案：
A
解析：
yt＋1－yt＝（t＋1）t/2－t（t－1）/2＝t＝f（t）。
yt＋1－yt＝（t＋1）t/2－t（t－1）/2＝t＝f（t）。
如果没有搜索结果，请直接 联系老师 获取答案。
相似问题和答案
第1题：
设R(t)表示可靠度函数，F(t)表示累积故障分布函数，则下列表述正确的有( )。
A．R(t)是[0，∞)区间内的非减函数，且0≤R(t)≤1
B．R(t)是[0，∞)区间内的非增函数，且0≤R(t)≤1
C．在[0，∞)区间内，R(t)+F(t)=1
D．F(t)在[0，∞)区间内的非减函数，且0≤F(t)≤1
E．F(t)在[0，∞)区间内是非增函数
正确答案：BCD
解析：可靠度R(t)随时间推移越来越低，是[0，∞)区间内的非增函数，且0≤R(t)≤1；而F(t)是[0，∞)区间内的非减函数，且0≤F(t)≤1；在[0，∞)区间内，R(t)+F(t)=1。
解析：可靠度R(t)随时间推移越来越低，是[0，∞)区间内的非增函数，且0≤R(t)≤1；而F(t)是[0，∞)区间内的非减函数，且0≤F(t)≤1；在[0，∞)区间内，R(t)+F(t)=1。
第2题：
对于直线趋势方程Yt=a＋bt,若已知∑t=0,∑tY=130,∑t²=169,a=6,则趋势方程中的b=( )
答案：0.7692
第3题：
已知f(t),为求f(t0－at)则下列运算错误的是(其中t0,a为正数)________。
;A.f(-at)左移t0
B.f(-at)右移t0
C.f(at)左移t0
D.f(at)右移t0
参考答案：ACD
第4题：
已知微分方程y’+y=f(x)，其中f(x)是R上的连续函数.
(Ⅰ)若f(x)=x，求方程的通解.
(Ⅱ)若f(x)是周期为T的函数，证明：方程存在唯一的以T为周期的解.
(Ⅰ)若f(x)=x，求方程的通解.
(Ⅱ)若f(x)是周期为T的函数，证明：方程存在唯一的以T为周期的解.
答案：
解析：
【解】(Ⅰ)若f(x)=x，则方程为y'+y=x通解为
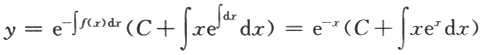
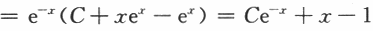
(Ⅱ)设y(x)为方程的任意解，则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T，有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0，有(e^x［y(x+T)-y(x)］)'=0，
即e^x［y(x+T)=y(x)］=C.取C=0得y(x+T)-y(x)=0，
y(x)为唯一以T为周期的解.
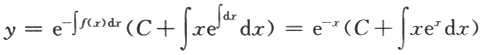
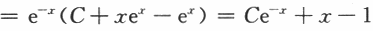
(Ⅱ)设y(x)为方程的任意解，则y'(x+T)+y(x+T)=f(x+T).
而f(x)周期为T，有f(x+T)=f(x).又y'(x)+y(x)=f(x).
因此y'(x+T)+y(x+T)-y'(x)-y(x)=0，有(e^x［y(x+T)-y(x)］)'=0，
即e^x［y(x+T)=y(x)］=C.取C=0得y(x+T)-y(x)=0，
y(x)为唯一以T为周期的解.
第5题：
已知f(t)是周期为T的函数,f(t)－f(t＋(5／2)T)的傅里叶级数中,不可能的是()。
A、正弦分量
B、余弦分量
C、奇次谐波分量
D、偶次谐波分量
参考答案：ABD
第6题：
已知函数 x(t)的傅里叶变换为 X(f),则函数 y(t)=2x(t)的傅里叶变换为( )。
A. 2X(t)
B. X(t )
C. X(f)
D. 2X(f)
答案D
第7题：
已知f(t)=t[u(t)－u(t－1)],求s(t)=f(t)*f(t),并画出s(t)的波形。
答案：对输入求拉普拉斯变换：F(s)=1+e(-s)对输出求拉普拉斯变换：Y(s)=[1-e(-s)]/s。所以H(s)=Y(s)/F(s)是h(t)的拉式变换，对H(s)求拉式反变换就是h(t)如果f(t)=δ(t)-δ(t1)的话，h(t)=u(t)，波形就是t0时的一条直线
第8题：
可靠度函数R(t)、累积故障分布函数F(t)和故障密度分布函数f(t)三者关系正确的有( )。
A.f(t)+F(t)=1
B.R(t)+F(t)=1
C.R(t)=tfudu
D.F(t)=0f(u)du
正确答案：BCD
第9题：
设参数方程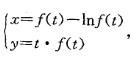
确定了y是x的函数，且f(t)存在，f(0) = 2，
f(0) = 2，则当t=0时，dy/dx的值等于：
A. 4/3 B. -4/3 C. -2 D. 2
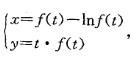确定了y是x的函数，且f(t)存在，f(0) = 2，
f(0) = 2，则当t=0时，dy/dx的值等于：
A. 4/3 B. -4/3 C. -2 D. 2
答案：C
解析：
提示:利用参数方程导数公式计算出dy/dx，代入t=0，得到t=0时的dy/dx值。计算如下：
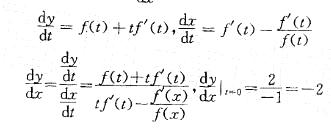
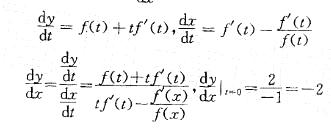
第10题：
已知象函数F（s）求解原函数f（t）的过程称为拉氏变换。（ ）
答案：错
解析：