设A为n阶对称矩阵,k为常数.试证kA仍为对称矩阵.
题目
设A为n阶对称矩阵,k为常数.试证kA仍为对称矩阵.
参考答案和解析
答案:
解析: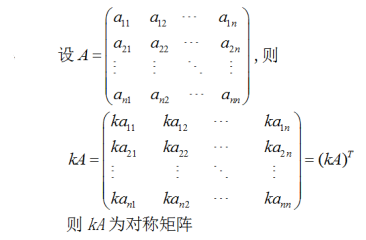

如果没有搜索结果,请直接 联系老师 获取答案。
相似问题和答案
第1题:
设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ).
A.二次型xTAx的负惯性指数零
B.存在n阶矩阵C,使得A=CTC
C.A没有负特征值
D.A与单位矩阵合同
参考答案:

第2题:
设A,B为,N阶实对称矩阵,则A与B合同的充分必要条件是().
A.r(A)=r(B)
B.|A|=|B|
C.A~B
D.A,B与同一个实对称矩阵合同
B.|A|=|B|
C.A~B
D.A,B与同一个实对称矩阵合同
答案:D
解析:
因为A,B与同一个实对称矩阵合同,则A,B合同.反之,若A,B合同,则A,B的正、负惯性指数相同,从而A,B与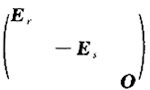 合同,选(D).
合同,选(D).
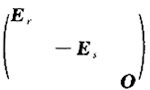 合同,选(D).
合同,选(D).第3题:
设A为非奇异对称矩阵,则____仍为对称矩阵。
A.A的转置
B.A的逆矩阵
C.3A
D.A与A的转置的乘积
参考答案:ABCD
第4题:
设n阶矩阵A与对角矩阵相似,则().
A.A的n个特征值都是单值
B.A是可逆矩阵
C.A存在n个线性无关的特征向量
D.A一定为n阶实对称矩阵
B.A是可逆矩阵
C.A存在n个线性无关的特征向量
D.A一定为n阶实对称矩阵
答案:C
解析:
矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量,A有n个单特征值只是其可对角化的充分而非必要条件,同样A是实对称阵也是其可对角化的充分而非必要条件,A可逆既非其可对角化的充分条件,也非其可对角化的必要条件,选(C).
第5题:
设A是一个n阶矩阵,那么是对称矩阵的是( ).


答案:A
解析: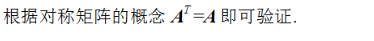
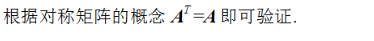
第6题:
设A是n阶实对称矩阵,则A有n个()特征值.
参考答案:实
第7题:
设A,B为n阶对称矩阵,下列结论不正确的是().
A.AB为对称矩阵
B.设A,B可逆,则A^-1+B^-1为对称矩阵
C.A+B为对称矩阵
D.kA为对称矩阵
B.设A,B可逆,则A^-1+B^-1为对称矩阵
C.A+B为对称矩阵
D.kA为对称矩阵
答案:A
解析:

第8题:
n阶对称矩阵A为正定矩阵的充分必要条件是()。
A、∣A∣0
B、存在n阶矩阵P,使得A=PTP
C、负惯性指数为0
D、各阶顺序主子式均为正数
参考答案:D
第9题:
设A为n阶矩阵,k为常数,则(kA)+等于().


答案:C
解析:

第10题:
n阶实对称矩阵A为正定矩阵,则下列不成立的是( )。
A.所有k级子式为正(k=1,2,…,n)
B.A的所有特征值非负
C.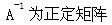
D.秩(A)=n
B.A的所有特征值非负
C.
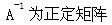
D.秩(A)=n
答案:A
解析:
